Chi-square test - less than 5 counts

[langmutsonia]

Hi there!

So I've got this sample of 2473 cases (judicial decisions), and I want to test if there is a possible relation between two nominal variables.

One variable stands for the type of decision (which entails 4 values: 1, 2, 3 and 4), and the other stands for the form of the decision (2 values: A and B).

I ran a Chi-Square test through "Crosstables" command :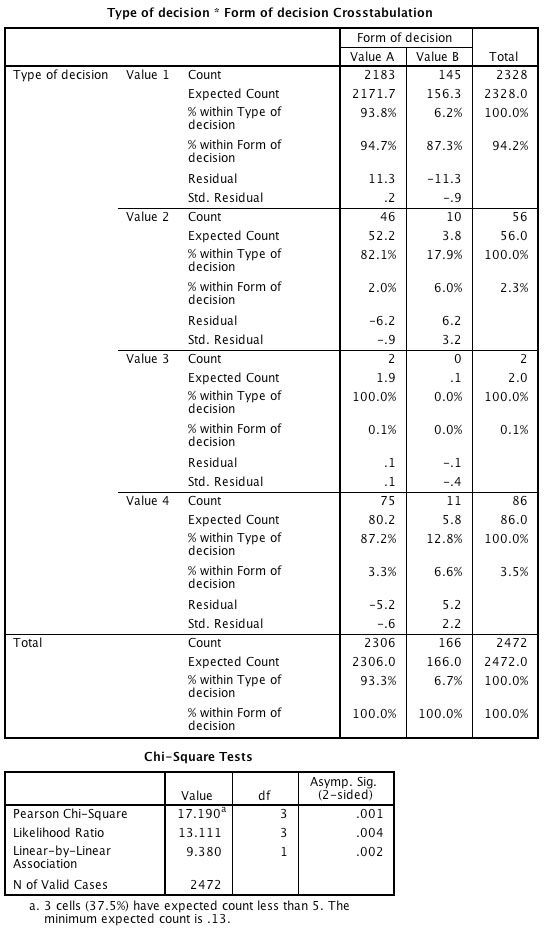





I also ran a Pearson Chi-Square test through "Custom tables" command, and it says: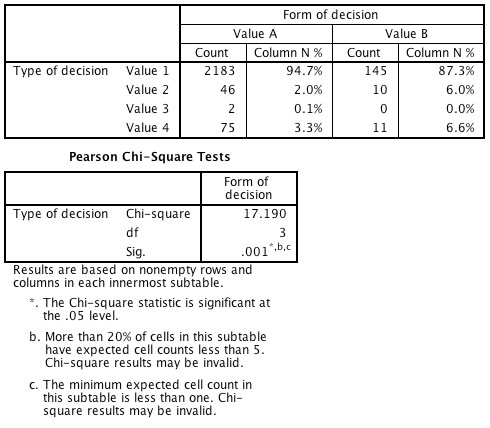




The thing is that in one of the decision types (Value 3) I've got only 2 counts for Value A and zero counts for Value B.

My question is: do you guys think it's still a valid test? What would you suggest if it is not the case?

I send the images of both results attached.

Many thanks in advance!

Cheers,

Langmut.

[Bruce Weaver]

Well, it does violate the usual guidelines for tables larger than 2x2 -- see https://sites.google.com/a/lakeheadu.ca/bweaver/Home/statistics/notes/chisqr_assumptions.

You could just omit the 2 cases with Value=3, or combine that level with another level if it makes sense to do so.  If you omit the 2 cases, you'll get chi-square = 17.033, df = 2, p = 0.0002 (at least according to the calculator at http://www.quantpsy.org/chisq/chisq.htm), and I think only 1 of the 6 (about 17%) expected counts will be < 5 (and all will be > 1).

HTH.

langmutsonia wrote

Hi there!

So I've got this sample of 2473 cases (judicial decisions), and I want to test if there is a possible relation between two nominal variables.

One variable stands for the type of decision (which entails 4 values: 1, 2, 3 and 4), and the other stands for the form of the decision (2 values: A and B).

I ran a Chi-Square test through "Crosstables" command :





I also ran a Pearson Chi-Square test through "Custom tables" command, and it says:




The thing is that in one of the decision types (Value 3) I've got only 2 counts for Value A and zero counts for Value B.

My question is: do you guys think it's still a valid test? What would you suggest if it is not the case?

I send the images of both results attached.

Many thanks in advance!

Cheers,

Langmut.

[Rich Ulrich]

However, it is easy to see that the "violations" for cells with
expected counts of 5 or less  result in less power than there might
be, rather than "too much power" which is what is considered
problematic.

In the first .jpg table cited, the standardized residuals are small
for all the small-Expectation cells -- Those residuals, squared,
are what add up (about) to the total chi-squared. The hazard,
for the rule of "5", is that dividing by a very small E will give an
inflated contribution to the total.  That does not happen; it is
not a problem. 

Instead, please notice, the small total N for Value=3  results
in the opposite bias:  The Ns are too tiny to contribute to the
total.  Thus (as Bruce shows), the overall X^2 test when you
drop that row has almost the same value, which has to have
a smaller p-level since the d.f.  is reduced to 2 from 3. 

--
Rich Ulrich

> Date: Fri, 8 Jun 2012 15:45:17 -0700

> From: [hidden email]
> Subject: Re: Chi-square test - less than 5 counts
> To: [hidden email]
>
> Well, it does violate the usual guidelines for tables larger than 2x2 -- see
> https://sites.google.com/a/lakeheadu.ca/bweaver/Home/statistics/notes/chisqr_assumptions.
>
> You could just omit the 2 cases with Value=3, or combine that level with
> another level if it makes sense to do so. If you omit the 2 cases, you'll
> get chi-square = 17.033, df = 2, p = 0.0002 (at least according to the
> calculator at http://www.quantpsy.org/chisq/chisq.htm), and I think only 1
> of the 6 (about 17%) expected counts will be < 5 (and all will be > 1).
>
> HTH.
>
>
> langmutsonia wrote
> >
> > Hi there!
> >
> > So I've got this sample of 2473 cases (judicial decisions), and I want to
> > test if there is a possible relation between two nominal variables.
> >
> > One variable stands for the type of decision (which entails 4 values: 1,
> > 2, 3 and 4), and the other stands for the form of the decision (2 values:
> > A and B).
> >
> > I ran a Chi-Square test through "Crosstables" command :
> >
> > http://spssx-discussion.1045642.n5.nabble.com/file/n5713603/crosstabs.jpg
> >
> >
> >
> > I also ran a Pearson Chi-Square test through "Custom tables" command, and
> > it says:
> >
> >
> > http://spssx-discussion.1045642.n5.nabble.com/file/n5713603/customtables.jpg
> >
> >
> > The thing is that in one of the decision types (Value 3) I've got only 2
> > counts for Value A and zero counts for Value B.
> >
> > My question is: do you guys think it's still a valid test? What would you
> > suggest if it is not the case?
> >
> > I send the images of both results attached.
> >
> > Many thanks in advance!
> >
> > Cheers,
> >

...