Error? the Command Syntax Ref entry on BVNOR
Error? the Command Syntax Ref entry on BVNOR
|
(Rick Oliver: I'm copying you, because you seem
to have a particular concern for SPSS documentation) From the Command Syntax Reference article "Universals", section "Random Variable and Distribution Functions": >BVNOR Bivariate normal distribution. The >bivariate normal distribution takes one >correlation parameter, r, which must be between >1 and 1, inclusive. The CDF and PDF functions >are available for this distribution and require two quantiles, q1 and q2. > >Two variables with correlation r and marginal >normal distributions with a mean of 0 and a >standard deviation of 1 have a bivariate normal distribution. I believe the condition in the last sentence is neither necessary nor sufficient for bivariate normality. First, a linear transform of a bivariate (or multivariate) normal distribution is (multi-)variate normal, though the transformed variable will not, in general, have marginal means 0 nor standard deviations 1. Second, here's an example of a bivariate distribution where each component is normally distributed with mean 0 and standard deviation 1, but the two together are not bivariate normal: Let X be random, normally distributed with mean 0 and standard deviation 1. Let a be a non-negative real number. Let Y = X if ABS(X) LT a, -X if ABS(X) GE a. Then, X and Y are both unit normal random variables. They can be given any correlation desired by adjusting a; correlation is +1 if a=0, approaches -1 as a->infinity. But the pair is NOT bivariate normal. In particular, X and Y are (clearly) not independent, even when their correlation is 0. (Correlation 0 is readily obtainable for a value of a which I'm not bothering to calculate.) -Onward, Richard ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
Good call, this thread on the Crossvalidated has the same discussion, Is it possible to have a pair of Gaussian random variables for which the joint distribution is not Gaussian? Here is an example image of other counterexamples.
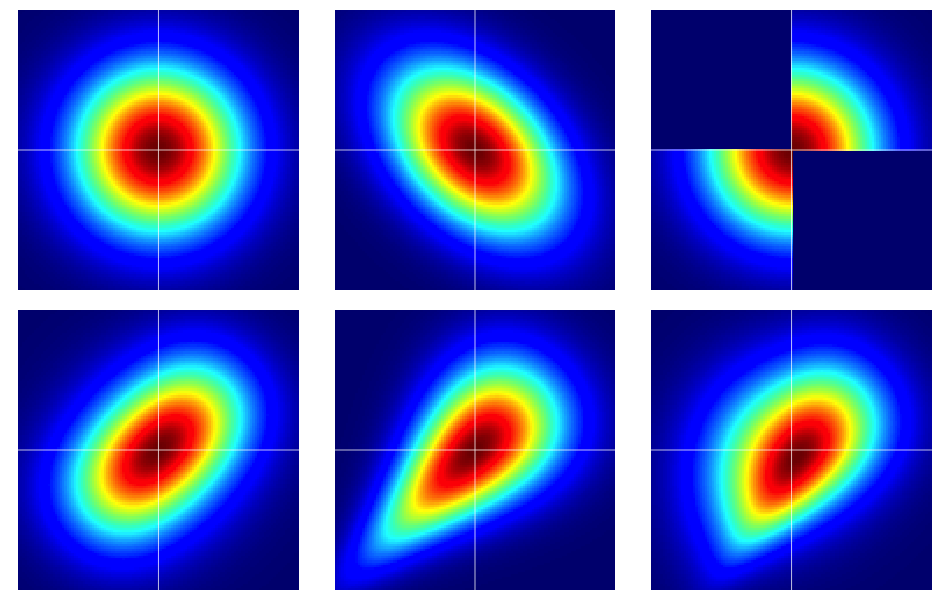 For those curious, here is what Richard's distribution looks like when "a" equals 1. 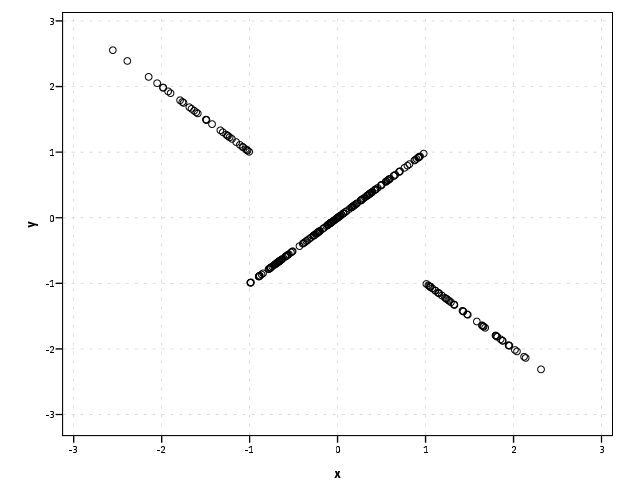 ********************************************. input program. loop #i = 1 to 100000. compute #a = 1. compute x = RV.NORMAL(0,1). do if ABS(x) < #a. compute y = x. else. compute y = -x. end if. end case. end loop. end file. end input program. freq var x y /format = notables /statistics = mean med stddev /ntiles = 4. correlations / vars = x y. formats x y (F1.0). temporary. sample 250 from 250. GRAPH /SCATTERPLOT(BIVAR)=x WITH y. exe. ********************************************. Can you provide an example where the marginals aren't normal but the bivariate is normal? (The necessary part) |
Re: Error? the Command Syntax Ref entry on BVNOR
|
At 02:33 PM 1/16/2014, Andy W wrote:
>Can you provide an example where the marginals aren't normal but the >bivariate is normal? (The necessary part) Absolutely not. But the Command Syntax Reference gives as the condition that the "two variables [have] marginal normal distributions with a mean of 0 and a standard deviation of 1". That the marginals are normal is necessary (but not sufficient); that they have mean 0 and standard deviation 1 is *not* necessary. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: Error? the Command Syntax Ref entry on BVNOR
|
I am somewhat confused by the original
message. While I don't pretend to know anything about the distribution,
this is what the CSR says in release 22:
"BVNOR. Bivariate normal distribution. The bivariate normal distribution takes real values and has one correlation parameter, ρ, which must be between –1 and 1, inclusive." That's all it says. Rick Oliver Senior Information Developer IBM Business Analytics (SPSS) E-mail: [hidden email] From: Richard Ristow <[hidden email]> To: [hidden email], Date: 01/16/2014 01:54 PM Subject: Re: Error? the Command Syntax Ref entry on BVNOR Sent by: "SPSSX(r) Discussion" <[hidden email]> At 02:33 PM 1/16/2014, Andy W wrote: >Can you provide an example where the marginals aren't normal but the >bivariate is normal? (The necessary part) Absolutely not. But the Command Syntax Reference gives as the condition that the "two variables [have] marginal normal distributions with a mean of 0 and a standard deviation of 1". That the marginals are normal is necessary (but not sufficient); that they have mean 0 and standard deviation 1 is *not* necessary. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: Error? the Command Syntax Ref entry on BVNOR
|
At 02:56 PM 1/16/2014, Rick Oliver wrote:
>While I don't pretend to know anything about the >distribution, this is what the CSR says in release 22: > >"BVNOR. Bivariate normal distribution. The >bivariate normal distribution takes real values >and has one correlation parameter, ñ, which must >be between 1 and 1, inclusive." > >That's all it says. So much for being behind the times. The sentence I quoted *is* in the CSR for release 14; it must have been noticed, and removed, since then. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: Error? the Command Syntax Ref entry on BVNOR
|
In reply to this post by Richard Ristow
What I find online (V21) does not say that. I copy --
"Two variables with a bivariate normal(ρ) distribution with correlation ρ have marginal normal distributions with a mean of 0 and a standard deviation of 1." http://pic.dhe.ibm.com/infocenter/spssstat/v21r0m0/index.jsp?topic=%2Fcom.ibm.spss.statistics.help%2Fcumdistfunctionlist.htm I suppose that this implies something like "*standard* bivariate normal." But in the context of the routines, Mean and SD are irrelevant, anyway. -- Rich Ulrich ---------------------------------------- > Date: Thu, 16 Jan 2014 10:31:01 -0500 > From: [hidden email] > Subject: Error? the Command Syntax Ref entry on BVNOR > To: [hidden email] > > (Rick Oliver: I'm copying you, because you seem > to have a particular concern for SPSS documentation) > > From the Command Syntax Reference article > "Universals", section "Random Variable and Distribution Functions": > >>BVNOR Bivariate normal distribution. The >>bivariate normal distribution takes one >>correlation parameter, r, which must be between >>-1 and 1, inclusive. The CDF and PDF functions >>are available for this distribution and require two quantiles, q1 and q2. >> >>Two variables with correlation r and marginal >>normal distributions with a mean of 0 and a >>standard deviation of 1 have a bivariate normal distribution. > > I believe the condition in the last sentence is > neither necessary nor sufficient for bivariate normality. > > First, a linear transform of a bivariate (or > multivariate) normal distribution is > (multi-)variate normal, though the transformed > variable will not, in general, have marginal > means 0 nor standard deviations 1. > > Second, here's an example of a bivariate > distribution where each component is normally > distributed with mean 0 and standard deviation 1, > but the two together are not bivariate normal: > > Let X be random, normally distributed with mean 0 and standard deviation 1. > > Let a be a non-negative real number. > > Let Y = X if ABS(X) LT a, -X if ABS(X) GE a. > > Then, X and Y are both unit normal random > variables. They can be given any correlation > desired by adjusting a; correlation is +1 if a=0, approaches -1 as a->infinity. > > But the pair is NOT bivariate normal. In > particular, X and Y are (clearly) not > independent, even when their correlation is 0. > (Correlation 0 is readily obtainable for a value > of a which I'm not bothering to calculate.) >... ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

