Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?

[DP_Sydney]

Hi,

Analysis question: I am seeking to determine whether there is a relationship between the extent of pigment in tail feathers of a particular bird species and the extent of pigment on 1) the foreneck (5 x 5 table, n = 40) and 2) the wings (4 x 5 table, n = 80). Pigment was scored on an ordinal scale from least to most pigment for each body region (5 levels for tail and foreneck, 4 levels for wing). Because of the small sample size. A chi-square contingency table is inappropriate because of the high proportion of expected values <5.

Option 1 - Fisher-Freeman-Halton Exact Test: Both contingency tables have a high number of zero cells: 12 in the 5 x 5 table, 6 in the 4 x 5 table. Is this a problem for this test?

Option 2 - Jonckheere–Terpstra test: At first glance, this test is appropriate since both my variables are ordinal variables and I expect a positive relationship (i.e. birds with more pigment on the tail are predicted to have more pigment on the foreneck or wing). However, I am not postulating a causal relationship between variables (i.e. pigment on tail vs pigment on foreneck/wing). Is this test appropriate for analyses where the independent and dependent variables are interchangeable? 

Any advice as to which option is the most suitable, and any other issues that I have not identified, is most welcome!

Thanks,
Dean

[Raimundas Vaitkevičius]

Hi, Dean,

as far as I know, Jonckheere–Terpstra test doesn't require any causal
relationship.

By the way, why don't you want to use some rank correlation coefficient?

Raimundas Vaitkevičius
Vytautas Magnus University, statistician


On Mon, Feb 15, 2016 at 8:50 AM, DP_Sydney <[hidden email]> wrote:

> Hi,
>
> *Analysis question*: I am seeking to determine whether there is a
> relationship between the extent of pigment in tail feathers of a particular
> bird species and the extent of pigment on 1) the foreneck (5 x 5 table, n =
> 40) and 2) the wings (4 x 5 table, n = 80). Pigment was scored on an ordinal
> scale from least to most pigment for each body region (5 levels for tail and
> foreneck, 4 levels for wing). Because of the small sample size. A chi-square
> contingency table is inappropriate because of the high proportion of
> expected values <5.
>
> *Option 1 - Fisher-Freeman-Halton Exact Test*: Both contingency tables have
> a high number of zero cells: 12 in the 5 x 5 table, 6 in the 4 x 5 table.
> /Is this a problem for this test?/
>
> *Option 2 - Jonckheere–Terpstra test*: At first glance, this test is
> appropriate since both my variables are ordinal variables and I expect a
> positive relationship (i.e. birds with more pigment on the tail are
> predicted to have more pigment on the foreneck or wing). However, I am not
> postulating a causal relationship between variables (i.e. pigment on tail vs
> pigment on foreneck/wing). /Is this test appropriate for analyses where the
> independent and dependent variables are interchangeable?/
>
> Any advice as to which option is the most suitable, and any other issues
> that I have not identified, is most welcome!
>
> Thanks,
> Dean
>
>
>
>
>
> --
> View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Fisher-Freeman-Halton-Exact-Test-or-Jonckheere-Terpstra-test-which-is-the-most-appropriate-tp5731524.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.
>
> =====================
> To manage your subscription to SPSSX-L, send a message to
> [hidden email] (not to SPSSX-L), with no body text except the
> command. To leave the list, send the command
> SIGNOFF SPSSX-L
> For a list of commands to manage subscriptions, send the command
> INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Rich Ulrich]

Neither test appears to be appropriate.  The FFH Exact Test does not consider
that either variable is ordinal.  The JT test does not handle ties well ... I have
not used it, but quick reading suggests that having a continuous outcome (and
small N) are two of the expectations. 

What is your total N?  How even, and how regular, are your marginal distributions?
If the distributions are either fairly uniform or bell-shaped, I would have no hesitation
of using the Pearson r as my main test. 

Other comments on your post:  The problems with (Expectations < 5)  for contingency
chi-squared owes to the generation of overly-BIG values when Expectations are too small,
thus providing a misleadingly large total.  If your overall contingency chi-squared is small,
you could accept that there is No Effect, if you were doing a proper test of your hypothesis. 
However, this is a very weak test of your hypothesis because it does not account for ordering.

Is the X2 test value large enough that a one d.f.  X2 test would be significant?  In that case, a
test that accounts for ordering has a chance of being significant.  - If the overall X2  is /really/
small, like, less that 3.83 needed for a 5% test, you could, indeed, fairly conclude that "There
is nothing here," regardless of the number of cells with tiny Expectations.

An Exact Test derived from the FET is not harmed by observed zeroes; it lacks power for you
because of it ignores the ordering (as I mentioned already).  Generally, one should keep in
mind that "Exact testing" for  r x k  tables is not a magic bullet, and not a unique proposition --
other methods (X2 contribution, instead of smallest likelihood used by Freeman-Halton) can
give other results, especially when there are highly skewed distributions.

--
Rich Ulrich

> Date: Sun, 14 Feb 2016 23:50:21 -0700

> From: [hidden email]
> Subject: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?
> To: [hidden email]
>
> Hi,
>
> *Analysis question*: I am seeking to determine whether there is a
> relationship between the extent of pigment in tail feathers of a particular
> bird species and the extent of pigment on 1) the foreneck (5 x 5 table, n =
> 40) and 2) the wings (4 x 5 table, n = 80). Pigment was scored on an ordinal
> scale from least to most pigment for each body region (5 levels for tail and
> foreneck, 4 levels for wing). Because of the small sample size. A chi-square
> contingency table is inappropriate because of the high proportion of
> expected values <5.
>
> *Option 1 - Fisher-Freeman-Halton Exact Test*: Both contingency tables have
> a high number of zero cells: 12 in the 5 x 5 table, 6 in the 4 x 5 table.
> /Is this a problem for this test?/
>
> *Option 2 - Jonckheere–Terpstra test*: At first glance, this test is
> appropriate since both my variables are ordinal variables and I expect a
> positive relationship (i.e. birds with more pigment on the tail are
> predicted to have more pigment on the foreneck or wing). However, I am not
> postulating a causal relationship between variables (i.e. pigment on tail vs
> pigment on foreneck/wing). /Is this test appropriate for analyses where the
> independent and dependent variables are interchangeable?/
>
> Any advice as to which option is the most suitable, and any other issues
> that I have not identified, is most welcome!
>
> Thanks,
> Dean

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[DP_Sydney]

Hi Rich and Raimundas,

Thanks for the comments.

The total sample size for the two tests is 80 (tail vs wing) and 40 (tail vs foreneck). The marginal distributions for each test are shown in the graphs below.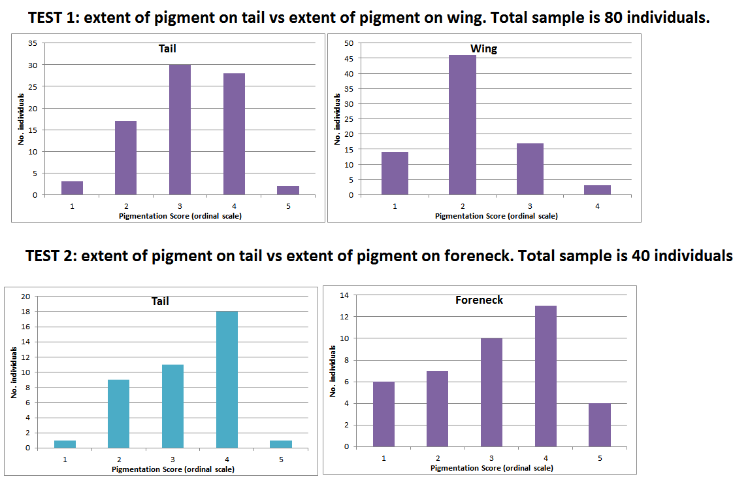

These distributions are bell-shaped for Test 1, and unimodal with a positive skew for Test 2. So you've convinced me that it is more appropriate to run a rank correlation on the data, which is also more intuitive (i.e. a correlation).

WRT to the Jonckheeere-Terpstra test, Rich you wrote "The JT test does not handle ties well ... I have not used it, but quick reading suggests that having a continuous outcome (and small N) are two of the expectations." I would like to read the text you refer to (this test may come in useful in the future, so I'm keen to learn more). I have not read anything about continuous outcomes, indeed the first reading I did about the JT test refers to its use in doubly-ordered contingency tables - i.e. ordinal dependent & ordinal independent (http://www.sussex.ac.uk/its/pdfs/SPSS_Exact_Tests_21.pdf). I'm also unsure what you mean by "ties".

Thanks also for the advice regarding the lack of power of the FFH Exact Test through it ignoring the ordinal nature of the variables, something I didn't appreciate.  

Cheers,
Dean

[Ryan]

I never obtained the original post but I would suggest examining a simple scatterplot. 

Apologies if that was already suggested. 

Ryan

Sent from my iPhone

On Feb 15, 2016, at 6:42 PM, Rich Ulrich <[hidden email]> wrote:

Neither test appears to be appropriate.  The FFH Exact Test does not consider
that either variable is ordinal.  The JT test does not handle ties well ... I have
not used it, but quick reading suggests that having a continuous outcome (and
small N) are two of the expectations. 

What is your total N?  How even, and how regular, are your marginal distributions?
If the distributions are either fairly uniform or bell-shaped, I would have no hesitation
of using the Pearson r as my main test. 

Other comments on your post:  The problems with (Expectations < 5)  for contingency
chi-squared owes to the generation of overly-BIG values when Expectations are too small,
thus providing a misleadingly large total.  If your overall contingency chi-squared is small,
you could accept that there is No Effect, if you were doing a proper test of your hypothesis. 
However, this is a very weak test of your hypothesis because it does not account for ordering.

Is the X2 test value large enough that a one d.f.  X2 test would be significant?  In that case, a
test that accounts for ordering has a chance of being significant.  - If the overall X2  is /really/
small, like, less that 3.83 needed for a 5% test, you could, indeed, fairly conclude that "There
is nothing here," regardless of the number of cells with tiny Expectations.

An Exact Test derived from the FET is not harmed by observed zeroes; it lacks power for you
because of it ignores the ordering (as I mentioned already).  Generally, one should keep in
mind that "Exact testing" for  r x k  tables is not a magic bullet, and not a unique proposition --
other methods (X2 contribution, instead of smallest likelihood used by Freeman-Halton) can
give other results, especially when there are highly skewed distributions.

--
Rich Ulrich

> Date: Sun, 14 Feb 2016 23:50:21 -0700

> From: [hidden email]
> Subject: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?
> To: [hidden email]
>
> Hi,
>
> *Analysis question*: I am seeking to determine whether there is a
> relationship between the extent of pigment in tail feathers of a particular
> bird species and the extent of pigment on 1) the foreneck (5 x 5 table, n =
> 40) and 2) the wings (4 x 5 table, n = 80). Pigment was scored on an ordinal
> scale from least to most pigment for each body region (5 levels for tail and
> foreneck, 4 levels for wing). Because of the small sample size. A chi-square
> contingency table is inappropriate because of the high proportion of
> expected values <5.
>
> *Option 1 - Fisher-Freeman-Halton Exact Test*: Both contingency tables have
> a high number of zero cells: 12 in the 5 x 5 table, 6 in the 4 x 5 table.
> /Is this a problem for this test?/
>
> *Option 2 - Jonckheere–Terpstra test*: At first glance, this test is
> appropriate since both my variables are ordinal variables and I expect a
> positive relationship (i.e. birds with more pigment on the tail are
> predicted to have more pigment on the foreneck or wing). However, I am not
> postulating a causal relationship between variables (i.e. pigment on tail vs
> pigment on foreneck/wing). /Is this test appropriate for analyses where the
> independent and dependent variables are interchangeable?/
>
> Any advice as to which option is the most suitable, and any other issues
> that I have not identified, is most welcome!
>
> Thanks,
> Dean

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Maguin, Eugene]

Might this dataset be a candidate for a permutation or randomization approach? If used, it would not address ordinality issue. The only thing it would do is to say that the observed test value is at the 'x' percentile of the distribution of test values resulting from all permutations of the dataset. Gene Maguin

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of DP_Sydney
Sent: Monday, February 15, 2016 8:57 PM
To: [hidden email]
Subject: Re: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?

Hi Rich and Raimundas,

Thanks for the comments.

The total sample size for the two tests is 40 (tail vs wing) and 80 (tail vs foreneck). The marginal distributions for each test are shown in the graphs below.
<http://spssx-discussion.1045642.n5.nabble.com/file/n5731529/SPSS_Discussion.png>
These distributions are bell-shaped for Test 1, and unimodal with a positive skew for Test 2. So you've convinced me that it is more appropriate to run a rank correlation on the data, which is also more intuitive (i.e. a correlation).

WRT to the Jonckheeere-Terpstra test, Rich you wrote "The JT test does not handle ties well ... I have not used it, but quick reading suggests that having a continuous outcome (and small N) are two of the expectations." I would like to read the text you refer to (this test may come in useful in the future, so I'm keen to learn more). I have not read anything about continuous outcomes, indeed the first reading I did about the JT test refers to its use in doubly-ordered contingency tables - i.e. ordinal dependent & ordinal independent (http://www.sussex.ac.uk/its/pdfs/SPSS_Exact_Tests_21.pdf). I'm also unsure what you mean by "ties".

Thanks also for the advice regarding the lack of power of the FFH Exact Test through it ignoring the ordinal nature of the variables, something I didn't
appreciate.  

Cheers,
Dean



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Fisher-Freeman-Halton-Exact-Test-or-Jonckheere-Terpstra-test-which-is-the-most-appropriate-tp5731524p5731529.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Bruce Weaver]

Regarding Rich's suggestion about using Pearson r, note that the test of linear-by-linear association that appears in the CROSSTABS output (when you include CHISQR on the /STATISTICS sub-command) is function of Pearson r.  You can get the details in Dave Howell's notes on ordinal Chi-square:

  https://www.uvm.edu/~dhowell/methods7/Supplements/OrdinalChiSq.html

And following up on Gene's suggestion about bootstrapping, if one could bootstrap the ordinal chi-square statistic, that might do the trick.  Unfortunately, it looks like bootstrapping does not work for the Chi-square tests generated by CROSSTABS.  Try this, for example:

DATA LIST list / R C Observations (3F5.0).
BEGIN DATA
0 1 25
1 1 13
2 1  9
3 1 10
4 1  6
0 2 31
1 2 21
2 2  6
3 2  2
4 2  3
END DATA.
DATASET NAME raw.

VARIABLE LABELS
 R "# of Traumatic Events"
 C "Dropout"
.
VALUE LABELS
 R 4 "4+" /
 C 1 "Drop out" 2 "Remain"
.
WEIGHT by Observations.
CROSSTABS R by C
 /CELLS=count row /STATISTICS=BTAU CTAU D CHISQ.

BOOTSTRAP.
CROSSTABS R by C
 /CELLS=count row /STATISTICS=BTAU CTAU D CHISQ.


Bootstrapping works for BTAU, CTAU and D, but not for CHISQ.  I wonder what the reason is for that?

Rich Ulrich wrote

Neither test appears to be appropriate.  The FFH Exact Test does not consider
that either variable is ordinal.  The JT test does not handle ties well ... I have
not used it, but quick reading suggests that having a continuous outcome (and
small N) are two of the expectations.  

What is your total N?  How even, and how regular, are your marginal distributions?
If the distributions are either fairly uniform or bell-shaped, I would have no hesitation
of using the Pearson r as my main test.  

Other comments on your post:  The problems with (Expectations < 5)  for contingency
chi-squared owes to the generation of overly-BIG values when Expectations are too small,
thus providing a misleadingly large total.  If your overall contingency chi-squared is small,
you could accept that there is No Effect, if you were doing a proper test of your hypothesis.  
However, this is a very weak test of your hypothesis because it does not account for ordering.

Is the X2 test value large enough that a one d.f.  X2 test would be significant?  In that case, a
test that accounts for ordering has a chance of being significant.  - If the overall X2  is /really/
small, like, less that 3.83 needed for a 5% test, you could, indeed, fairly conclude that "There
is nothing here," regardless of the number of cells with tiny Expectations.

An Exact Test derived from the FET is not harmed by observed zeroes; it lacks power for you
because of it ignores the ordering (as I mentioned already).  Generally, one should keep in
mind that "Exact testing" for  r x k  tables is not a magic bullet, and not a unique proposition --
other methods (X2 contribution, instead of smallest likelihood used by Freeman-Halton) can
give other results, especially when there are highly skewed distributions.

--
Rich Ulrich

> Date: Sun, 14 Feb 2016 23:50:21 -0700
> From: [hidden email]
> Subject: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?
> To: [hidden email]
>
> Hi,
>
> *Analysis question*: I am seeking to determine whether there is a
> relationship between the extent of pigment in tail feathers of a particular
> bird species and the extent of pigment on 1) the foreneck (5 x 5 table, n =
> 40) and 2) the wings (4 x 5 table, n = 80). Pigment was scored on an ordinal
> scale from least to most pigment for each body region (5 levels for tail and
> foreneck, 4 levels for wing). Because of the small sample size. A chi-square
> contingency table is inappropriate because of the high proportion of
> expected values <5.
>
> *Option 1 - Fisher-Freeman-Halton Exact Test*: Both contingency tables have
> a high number of zero cells: 12 in the 5 x 5 table, 6 in the 4 x 5 table.
> /Is this a problem for this test?/
>
> *Option 2 - Jonckheere–Terpstra test*: At first glance, this test is
> appropriate since both my variables are ordinal variables and I expect a
> positive relationship (i.e. birds with more pigment on the tail are
> predicted to have more pigment on the foreneck or wing). However, I am not
> postulating a causal relationship between variables (i.e. pigment on tail vs
> pigment on foreneck/wing). /Is this test appropriate for analyses where the
> independent and dependent variables are interchangeable?/  
>
> Any advice as to which option is the most suitable, and any other issues
> that I have not identified, is most welcome!
>
> Thanks,
> Dean

     
=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Rich Ulrich]

Gene,

Asking for a "permutation approach" is redundant to what has been posted.  The
so-called Exact-test approach is permutation, for which we use randomization when the
permutation-universe is too large. 

As you say, it does not address ordinality; it only seeks to replace the overall contingency
chi-squared (for which the power is small).

What I was trying to say about the permutation tests:  They need to order the outcomes;
when the table is larger than 2x2, there are several competing criteria for "order" that do
not necessarily give the same order.

--
Rich Ulrich

> Date: Tue, 16 Feb 2016 16:33:13 +0000
> From: [hidden email]
> Subject: Re: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?
> To: [hidden email]
>
> Might this dataset be a candidate for a permutation or randomization approach? If used, it would not address ordinality issue. The only thing it would do is to say that the observed test value is at the 'x' percentile of the distribution of test values resulting from all permutations of the dataset. Gene Maguin

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Rich Ulrich]

Well, my default recommendation, given nothing too odd in the distributions,
was to use an ordinary Pearson r on the 1-5 scores, not on the rank-transformed
scores.

The Spearman rho is exactly the Pearson r, computed on appropriately
transformed scores (use the average rank for each group).  The question of
transformation by rank, as I see it, is whether the transformed scores have
"better intervals" than the raw scores.  The quality of the intervals is usually
a subjective matter (unless there is test-retest data on hand).

ON RANK-TRANSFORMATIONs
From the URl cited, I get marginal counts for several tables, Ns of 80, 40, and 80:
a. (1, 17, 20, 18, 2);             (1, 9, 11, 18, 1);  and (14, 46, 17, 3). 
Average Ranks, cumulating left to right:
(2, 12, 30.5, 49.5, 59.5); (1, 6, 16, 35, 40); and (7.5, 37.5, 69, 79), respectively.
b. Intervals between adjacent categories:
(10, 18.5, 19, 10);         (5, 10, 9, 5);           and (30, 31.5, 10). [Or: 1221, 1221, 331]
Re-scored to simpler integers with highly-similar relative spacing:
 c. ( 0, 1, 3, 5, 6);              ( 0, 1, 3, 5, 6)<same>;  and (1, 4, 7, 8).
Re-scored to intervals that are mostly integer:
 d.  (0.3, 1, 2, 3, 3.7);         ( 0.3, 1, 2, 3, 3.7 );      and (0, 1, 2, 2.3).

 The question I ask for considering the rank-transform is whether the scoring
in (c) or (d), which are equivalent to each other, is to be preferred on logical
grounds to the scores of 1-5 (or 0-4);  or 1-4 (or 0-3).  Lines (c) and (d) provide
less importance to the extreme scores when you conduct an ANOVA or correlation: 
Is that desirable?  On occasion, I say "yes" -- when the extremes are of doubtful validity.

ON J-T TEST, and other rank tests.
On the J-T, I read whatever SPSS has in its manual and I read another description on-line.
J-T described an approximate test for large samples, using estimates for variance.  These
rank-test variance solutions were shown to be problematic by Conover in the 1980s.  He
and his co-author showed that performing ANOVA on the rank-transformed scores is always
a very close approximation, and often is an improvement, over the test-size achieved by
the adaptions that are made for "ties" -- where a tie is what you have for two scores that
are identical.  For small enough samples, of course, there originally were tables for p-values.
Computers can do better, if the problem is important enough that someone programs for it.

The worked-example I found used a nearly-continuous outcome and included formulas
(including, accounting somewhat for ties); I assumed that the there are the usual problems
with ties.

Rank tests were initially admired for their performance in continuous-scored samples;
how they do with ties is less admirable. 

ON THE POWER OF J x K CONTINGENCY TESTS  or Exact solutions.
Mantel flew in once a week to teach one of the stat courses that I took in grad school.

He passed out reprints of maybe 150 of his papers, and at least 100 of them were uses
of "tests using a 1 d.f.  chi-squared"; his point, over and over, was that you have most
power when one test is carried by 1 d.f.   If you are using 2 d.f. for your test (or more),
you are /almost always/  testing more than one hypothesis, at least implicitly.

--
Rich Ulrich

> Date: Mon, 15 Feb 2016 18:56:57 -0700

> From: [hidden email]
> Subject: Re: Fisher-Freeman-Halton Exact Test or Jonckheere–Terpstra test - which is the most appropriate?
> To: [hidden email]
>
> Hi Rich and Raimundas,
>
> Thanks for the comments.
>
> The total sample size for the two tests is 40 (tail vs wing) and 80 (tail vs
> foreneck). The marginal distributions for each test are shown in the graphs
> below.
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5731529/SPSS_Discussion.png>
> These distributions are bell-shaped for Test 1, and unimodal with a positive
> skew for Test 2. So you've convinced me that it is more appropriate to run a
> rank correlation on the data, which is also more intuitive (i.e. a
> correlation).
>
> WRT to the Jonckheeere-Terpstra test, Rich you wrote "The JT test does not
> handle ties well ... I have not used it, but quick reading suggests that
> having a continuous outcome (and small N) are two of the expectations." I
> would like to read the text you refer to (this test may come in useful in
> the future, so I'm keen to learn more). I have not read anything about
> continuous outcomes, indeed the first reading I did about the JT test refers
> to its use in doubly-ordered contingency tables - i.e. ordinal dependent &
> ordinal independent
> (http://www.sussex.ac.uk/its/pdfs/SPSS_Exact_Tests_21.pdf). I'm also unsure
> what you mean by "ties".
>
> Thanks also for the advice regarding the lack of power of the FFH Exact Test
> through it ignoring the ordinal nature of the variables, something I didn't
> appreciate.
>
> Cheers,
> Dean

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[DP_Sydney]

I have performed Spearman Rank Correlations for both tests using a one-tailed hypothesis as I expect a priori that birds with more heavily pigmented tails will also have more heavily pigmented wings or forenecks.

The following graph shows a scatterplot of the data. As ordinal variables are used there are many duplicates of particular combinations of X-Y values. So the data points have been converted to different sized circles representing the number of individuals (i.e. sample size for that particular X-Y combination) as follows:
WING (= MANUS, top): 1 (smallest circle), 2-4, 5-9, 14, 20 (largest circle)
FORENECK (bottom): 1 (smallest), 2, 3, 4, 9 (largest)
Note "R6" in the x-axis title indicates the outer feather of the TAIL.



Results of the Spearman Rank Correlations are:
Wing: ρ = 0.193, t78 = 1.74, P = 0.043
Foreneck: ρ = 0.432, t38 = 2.95, P = 0.003

Calculating Pearson's Correlations for the data (for the sake of this thread):
Wing: r = 0.193, t78 = 1.73, P = 0.044
Foreneck: r = 0.3949, t38 = 2.65, P = 0.006

The results are very similar, including both correlation coefficient, test statistic and P value. The one exception is for the foreneck ρ > r, which according to comments in this post suggests the relationship may not be linear.

Given the data are ordinal scores I consider the Spearman Rank Correlation more appropriate to report.

NOTE: Two-tailed P-values are significant only for Foreneck. But THIS WAS NOT a deciding factor in calculating one-tailed tests a priori.

NOTE: the intervals used for the ordinal scores for the tail and foreneck are reasonably evenly spaced (i.e. the increase in level of pigmentation between adjacent scores is similar across all adjacent scores, EXCEPT for the first two scores for the tail which are much more similar to one another). The manus score is less 'evenly spaced'.