General Linear Model using proportions as raw data - transformation needed?

[DP_Sydney]

Hi,

I have become confused in my reading of analysis of proportions. I was all set to analyse my data using a general linear model after transforming the proportions using an arcsine-square root transformation, but now I'm not sure if this is a correct approach and more importantly why/why not!

The data comprises time-activity budgets of group-living animals. Each group was followed for a variable period of time (30min to 6hours) and the time they spent alone or with another group was calculated as a proportion of the total observation time. I collected data from multiple groups in six months of two consecutive years (not all groups were present or sampled in each month, nor visited an equal number of times each month). I also collected data from two months in a third year, but because of the gaps in the sampling I'm unsure whether I can include this third year in the same analysis.

I wish to analyse whether the time groups spend associating with one another differs among months within a year and between years (i.e. is it temporally variable? and if so, is this consistent between years?).

The analysis I envisaged was a general linear model with the following parameters:
1) month as a fixed factor
2) year as a random factor
3) month*year as an interaction term
4) group identity as a random factor
5) 'proportion time groups associating' as the response variable once arcsine-square root transformed
Sample sizes were as follows:
Year 1:
Jul - n=6 (first month of study so sampling was poor)
Aug - n=13
Sep - n=15
Oct - n=12
Nov - n=11
Apr - n=20
Year 2:
Jul - n=33
Aug - n=23
Sep - n=4
Oct - n=30
Nov - n=14
Apr - n=14
Year 3:
Aug - n=19
Apr - n=19

QUESTIONS:
1) Is transformation of proportions necessary/appropriate?
2) Can I include the third year in the one analysis? Or should I run a second analysis including only data for Aug and Apr of the three years?

Any advice would be greatly appreciated.

Thanks,
Dean

[Bruce Weaver]

I'm not going to attempt to deal with everything in your post, but here a are a couple quick comments.  

1. It appears you are wanting to use GENLINMIXED.  I just checked the CSR manual (aka the FM) to see if GENLINMIXED allows an "events-of-trials" outcome variable the way GENLIN does.  Sadly, it does not.  

2. If you are going to transform, you might consider using the logit transformation rather than arcsine-square root.  Here is an article (with a catchy title) that says more on that topic.  ;-)

  http://byrneslab.net/classes/biol607/readings/Wharton_Hui_2011_Ecology.pdf

HTH.

DP_Sydney wrote

Hi,

I have become confused in my reading of analysis of proportions. I was all set to analyse my data using a general linear model after transforming the proportions using an arcsine-square root transformation, but now I'm not sure if this is a correct approach and more importantly why/why not!

The data comprises time-activity budgets of group-living animals. Each group was followed for a variable period of time (30min to 6hours) and the time they spent alone or with another group was calculated as a proportion of the total observation time. I collected data from multiple groups in six months of two consecutive years (not all groups were present or sampled in each month, nor visited an equal number of times each month). I also collected data from two months in a third year, but because of the gaps in the sampling I'm unsure whether I can include this third year in the same analysis.

I wish to analyse whether the time groups spend associating with one another differs among months within a year and between years (i.e. is it temporally variable? and if so, is this consistent between years?).

The analysis I envisaged was a general linear model with the following parameters:
1) month as a fixed factor
2) year as a random factor
3) month*year as an interaction term
4) group identity as a random factor
5) 'proportion time groups associating' as the response variable once arcsine-square root transformed
Sample sizes were as follows:
Year 1:
Jul - n=6 (first month of study so sampling was poor)
Aug - n=13
Sep - n=15
Oct - n=12
Nov - n=11
Apr - n=20
Year 2:
Jul - n=33
Aug - n=23
Sep - n=4
Oct - n=30
Nov - n=14
Apr - n=14
Year 3:
Aug - n=19
Apr - n=19

QUESTIONS:
1) Is transformation of proportions necessary/appropriate?
2) Can I include the third year in the one analysis? Or should I run a second analysis including only data for Aug and Apr of the three years?

Any advice would be greatly appreciated.

Thanks,
Dean

[Alex Reutter]

GENLINMIXED does allow events of trials.  If you specify a TRIALS keyword, it automatically treats the TARGET as the events field.

GENLINMIXED
 /FIELDS
   TARGET = fieldName
   [TRIALS = {NONE**          }]
             {VALUE(number)   }
             {FIELD(fieldName)}


For example (http://www-01.ibm.com/support/knowledgecenter/SSLVMB_23.0.0/spss/advanced/syn_genlinmixed_examples.dita):

Binary probit model

GENLINMIXED
 /FIELDS TARGET=response TRIALS=nsubj
 /TARGET_OPTIONS DISTRIBUTION=BINOMIAL LINK=PROBIT
 /FIXED EFFECTS=site value.

• The procedure fits a model for the number of responses response within trials nsubj using site and value as main effects.
• The TARGET_OPTIONS specification assumes that response within nsubj has a binomial distribution. A probit link function relates the distribution of the target to a linear combination of the predictors, including an intercept term.

From:        Bruce Weaver <[hidden email]>
To:        [hidden email]
Date:        07/21/2015 09:11 AM
Subject:        Re: General Linear Model using proportions as raw data - transformation needed?
Sent by:        "SPSSX(r) Discussion" <[hidden email]>

---

1. It appears you are wanting to use GENLINMIXED.  I just checked the CSR
manual (aka the FM) to see if GENLINMIXED allows an "events-of-trials"
outcome variable the way GENLIN does.  Sadly, it does not.  



===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Bruce Weaver]

Ah, very good!  Thanks Alex.  I'm glad I was wrong about that.  ;-)

Alex Reutter wrote

GENLINMIXED does allow events of trials.  If you specify a TRIALS keyword,
it automatically treats the TARGET as the events field.

GENLINMIXED
  /FIELDS
    TARGET = fieldName
    [TRIALS = {NONE**          }]
              {VALUE(number)   }
              {FIELD(fieldName)}


For example (
http://www-01.ibm.com/support/knowledgecenter/SSLVMB_23.0.0/spss/advanced/syn_genlinmixed_examples.dita
):

Binary probit model
GENLINMIXED
  /FIELDS TARGET=response TRIALS=nsubj
  /TARGET_OPTIONS DISTRIBUTION=BINOMIAL LINK=PROBIT
  /FIXED EFFECTS=site value.
The procedure fits a model for the number of responses response within
trials nsubj using site and value as main effects.
The TARGET_OPTIONS specification assumes that response within nsubj has a
binomial distribution. A probit link function relates the distribution of
the target to a linear combination of the predictors, including an
intercept term.




From:   Bruce Weaver <[hidden email]>
To:     [hidden email]
Date:   07/21/2015 09:11 AM
Subject:        Re: General Linear Model using proportions as raw data -
transformation needed?
Sent by:        "SPSSX(r) Discussion" <[hidden email]>



1. It appears you are wanting to use GENLINMIXED.  I just checked the CSR
manual (aka the FM) to see if GENLINMIXED allows an "events-of-trials"
outcome variable the way GENLIN does.  Sadly, it does not.





=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[DP_Sydney]

Hi Bruce,

Thanks for the link to the paper and suggesting GENLINMIXED. I will have a read of the paper and do some research on what GENLINMIXED is all about, but I wonder if you can clarify what you mean by "events-of-trials"?

Thanks,

Dean

---

Date: Tue, 21 Jul 2015 06:09:49 -0700
From: [hidden email]
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

I'm not going to attempt to deal with everything in your post, but here a are a couple quick comments.  

1. It appears you are wanting to use GENLINMIXED.  I just checked the CSR manual (aka the FM) to see if GENLINMIXED allows an "events-of-trials" outcome variable the way GENLIN does.  Sadly, it does not.  

2. If you are going to transform, you might consider using the logit transformation rather than arcsine-square root.  Here is an article (with a catchy title) that says more on that topic.  ;-)

  http://byrneslab.net/classes/biol607/readings/Wharton_Hui_2011_Ecology.pdf

HTH.

DP_Sydney wrote

Hi,

I have become confused in my reading of analysis of proportions. I was all set to analyse my data using a general linear model after transforming the proportions using an arcsine-square root transformation, but now I'm not sure if this is a correct approach and more importantly why/why not!

The data comprises time-activity budgets of group-living animals. Each group was followed for a variable period of time (30min to 6hours) and the time they spent alone or with another group was calculated as a proportion of the total observation time. I collected data from multiple groups in six months of two consecutive years (not all groups were present or sampled in each month, nor visited an equal number of times each month). I also collected data from two months in a third year, but because of the gaps in the sampling I'm unsure whether I can include this third year in the same analysis.

I wish to analyse whether the time groups spend associating with one another differs among months within a year and between years (i.e. is it temporally variable? and if so, is this consistent between years?).

The analysis I envisaged was a general linear model with the following parameters:
1) month as a fixed factor
2) year as a random factor
3) month*year as an interaction term
4) group identity as a random factor
5) 'proportion time groups associating' as the response variable once arcsine-square root transformed
Sample sizes were as follows:
Year 1:
Jul - n=6 (first month of study so sampling was poor)
Aug - n=13
Sep - n=15
Oct - n=12
Nov - n=11
Apr - n=20
Year 2:
Jul - n=33
Aug - n=23
Sep - n=4
Oct - n=30
Nov - n=14
Apr - n=14
Year 3:
Aug - n=19
Apr - n=19

QUESTIONS:
1) Is transformation of proportions necessary/appropriate?
2) Can I include the third year in the one analysis? Or should I run a second analysis including only data for Aug and Apr of the three years?

Any advice would be greatly appreciated.

Thanks,
Dean

---

If you reply to this email, your message will be added to the discussion below:

http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730205.html

To unsubscribe from General Linear Model using proportions as raw data - transformation needed?, click here.
NAML

[Bruce Weaver]

Dean, in your case:

Events = minutes spent alone
Trials = total time in minutes

But upon further thought about your problem, the events-of-trials approach typically assumes that both the events and trials variables are discrete counts (e.g., some number of Heads in a total number of coin flips).  Technically, that's not so for your two time variables.  So I don't know whether GENLINMIXED can handle them as true continuous variables.  I don't see anything in the FM that says it cannot:

---- Start of excerpt from the FM ----
TRIALS = NONE** | VALUE(number) | FIELD(field). If the model response can be expressed as the
number of events occurring within a number of trials, then the TARGET keyword specifies the number of
events and TRIALS specifies the number of trials. Use VALUE with the number of trials in parentheses if
the number of trials is fixed for all subjects and FIELD with a field name in parentheses if the number of
trials varies across subjects and there is a field containing the number of trials.

The procedure automatically computes the ratio of the events field over the trials field or number.
Technically, the procedure treats the events field as the target in the sense that predicted values and
residuals are based on the events field rather than the events/trials ratio.
---- End of excerpt from the FM ----

So, it's an empirical question.  In other words, give it a try and see what happens.

DP_Sydney wrote

Hi Bruce,
Thanks for the link to the paper and suggesting GENLINMIXED. I will have a read of the paper and do some research on what GENLINMIXED is all about, but I wonder if you can clarify what you mean by "events-of-trials"?
Thanks,Dean

Date: Tue, 21 Jul 2015 06:09:49 -0700
From: [hidden email]
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?



        I'm not going to attempt to deal with everything in your post, but here a are a couple quick comments.  


1. It appears you are wanting to use GENLINMIXED.  I just checked the CSR manual (aka the FM) to see if GENLINMIXED allows an "events-of-trials" outcome variable the way GENLIN does.  Sadly, it does not.  


2. If you are going to transform, you might consider using the logit transformation rather than arcsine-square root.  Here is an article (with a catchy title) that says more on that topic.  ;-)


  http://byrneslab.net/classes/biol607/readings/Wharton_Hui_2011_Ecology.pdf

HTH.




DP_Sydney wrote
Hi,


I have become confused in my reading of analysis of proportions. I was all set to analyse my data using a general linear model after transforming the proportions using an arcsine-square root transformation, but now I'm not sure if this is a correct approach and more importantly why/why not!


The data comprises time-activity budgets of group-living animals. Each group was followed for a variable period of time (30min to 6hours) and the time they spent alone or with another group was calculated as a proportion of the total observation time. I collected data from multiple groups in six months of two consecutive years (not all groups were present or sampled in each month, nor visited an equal number of times each month). I also collected data from two months in a third year, but because of the gaps in the sampling I'm unsure whether I can include this third year in the same analysis.


I wish to analyse whether the time groups spend associating with one another differs among months within a year and between years (i.e. is it temporally variable? and if so, is this consistent between years?).


The analysis I envisaged was a general linear model with the following parameters:

1) month as a fixed factor

2) year as a random factor

3) month*year as an interaction term

4) group identity as a random factor

5) 'proportion time groups associating' as the response variable once arcsine-square root transformed

Sample sizes were as follows:

Year 1:

Jul - n=6 (first month of study so sampling was poor)

Aug - n=13

Sep - n=15

Oct - n=12

Nov - n=11

Apr - n=20

Year 2:

Jul - n=33

Aug - n=23

Sep - n=4

Oct - n=30

Nov - n=14

Apr - n=14

Year 3:

Aug - n=19

Apr - n=19


QUESTIONS:

1) Is transformation of proportions necessary/appropriate?

2) Can I include the third year in the one analysis? Or should I run a second analysis including only data for Aug and Apr of the three years?


Any advice would be greatly appreciated.


Thanks,

Dean




       
       
       
                                --

Bruce Weaver

[hidden email]

http://sites.google.com/a/lakeheadu.ca/bweaver/

"When all else fails, RTFM."


NOTE: My Hotmail account is not monitored regularly.

To send me an e-mail, please use the address shown above.


                       
       

       

       
       
                If you reply to this email, your message will be added to the discussion below:
                http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730205.html
       
       
               
                To unsubscribe from General Linear Model using proportions as raw data - transformation needed?, click here.

                NAML

[Rich Ulrich]

Since you do not have events, you might want to go back to the idea of
a single transformation, for which Bruce earlier suggested the logit -- and
gave a good reference for preferring logit over the arcsin sqrt (p).

You might be stumbling over the practicality, that the arcsin can deal with
0 and 100%, where the logit cannot.  Plus, your data seems to include
time periods that vary from 30 minutes to 300 minutes. 

When there is a constant time, it is easier to decide on how to accommodate
the extremes.  There are several options.  It is possible to replace them: so
that 0 and 1.0 become, say, 0.01 and 0.99  (or some such). 

That does not work so well when intervals vary.  In your data, (.01, .99)  looks
okay for an interval of 30 minutes, but would not be good for 300 minutes
since "1 minute" would yield a more extreme logit. 

I think I would go with the idea of the scoring that is used for Ranks; effectively,
add-on  0.5 to ranks 0 to 99  before dividing by 100.   For yours, you might
work from either Minutes (0-30; or 0-300) or from raw proportions (0-100%).
In either case, the idea is to take some Epsilon/2  as the distance from the
extreme; and divide by the (total + epsilon).  Thus, using 5% to adjust the
raw proportions, or 5 minutes to adjust the raw Times,  you could use

  AdjustedProp=  ((EventTime/ObsTime) + 0.025)/ 1.05
or
  AdjustedProp=   (EventTime+ 2.5)/ (ObsTime+ 5.0)   .

Then you compute the logit of the Adjusted Proportion in the usual way, log (p/(1-p)).

--
Rich Ulrich

> Date: Wed, 22 Jul 2015 04:42:37 -0700

> From: [hidden email]
> Subject: Re: General Linear Model using proportions as raw data - transformation needed?
> To: [hidden email]
>
> Dean, in your case:
>
> Events = minutes spent alone
> Trials = total time in minutes
>
> But upon further thought about your problem, the events-of-trials approach
> typically assumes that both the events and trials variables are discrete
> counts (e.g., some number of Heads in a total number of coin flips).
> Technically, that's not so for your two time variables. So I don't know
> whether GENLINMIXED can handle them as true continuous variables. I don't
> see anything in the FM that says it cannot:

[snip]

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Maguin, Eugene]

I’d like to kibbitz (what does that Yiddish? word mean anyway?) from the sidelines. Might one think of time intervals as being  trials. So a 30 minute observation period would be defined to consist of 30 one minute events during which an interaction may start or continue. I would imagine that the conventional concept of a trial is one where knowing the result of the current trial offers no information about the outcome of the next trial but perhaps not.

Gene Maguin

 

 

From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of Rich Ulrich
Sent: Wednesday, July 22, 2015 12:48 PM
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

 

Since you do not have events, you might want to go back to the idea of
a single transformation, for which Bruce earlier suggested the logit -- and
gave a good reference for preferring logit over the arcsin sqrt (p).

You might be stumbling over the practicality, that the arcsin can deal with
0 and 100%, where the logit cannot.  Plus, your data seems to include
time periods that vary from 30 minutes to 300 minutes. 

When there is a constant time, it is easier to decide on how to accommodate
the extremes.  There are several options.  It is possible to replace them: so
that 0 and 1.0 become, say, 0.01 and 0.99  (or some such). 

That does not work so well when intervals vary.  In your data, (.01, .99)  looks
okay for an interval of 30 minutes, but would not be good for 300 minutes
since "1 minute" would yield a more extreme logit. 

I think I would go with the idea of the scoring that is used for Ranks; effectively,
add-on  0.5 to ranks 0 to 99  before dividing by 100.   For yours, you might
work from either Minutes (0-30; or 0-300) or from raw proportions (0-100%).
In either case, the idea is to take some Epsilon/2  as the distance from the
extreme; and divide by the (total + epsilon).  Thus, using 5% to adjust the
raw proportions, or 5 minutes to adjust the raw Times,  you could use

  AdjustedProp=  ((EventTime/ObsTime) + 0.025)/ 1.05
or
  AdjustedProp=   (EventTime+ 2.5)/ (ObsTime+ 5.0)   .

Then you compute the logit of the Adjusted Proportion in the usual way, log (p/(1-p)).

--
Rich Ulrich

> Date: Wed, 22 Jul 2015 04:42:37 -0700
> From: [hidden email]
> Subject: Re: General Linear Model using proportions as raw data - transformation needed?
> To: [hidden email]
>
> Dean, in your case:
>
> Events = minutes spent alone
> Trials = total time in minutes
>
> But upon further thought about your problem, the events-of-trials approach
> typically assumes that both the events and trials variables are discrete
> counts (e.g., some number of Heads in a total number of coin flips).
> Technically, that's not so for your two time variables. So I don't know
> whether GENLINMIXED can handle them as true continuous variables. I don't
> see anything in the FM that says it cannot:
[snip]

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[DP_Sydney]

Hi Rich and Bruce,

Thanks very much for the advice. I have read David Warton's paper (thanks very much for the link Bruce!) and have attempted to digest the issue I am faced with. To me, it doesn't seem like my data conform to a typical 'trials and events' format, but is a binomial proportion as described by Warton and thus a logit transform, as you have both suggested, would be appropriate. But, I do indeed have a problem with many 0.0 and 1.0 proportions in my dataset: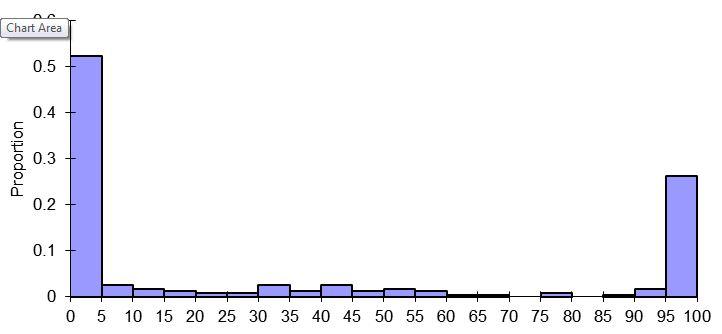

Histogram of raw proportions.

I like the idea of using an adjusted proportion so I can apply a logit transformation. Rich, could you please confirm that the adjustment needs to be made to ALL values, not just values of 0.0 and 1.0?

From there, I originally expected I could run an 'ANOVA-type' general linear mixed model with month (fixed), year (random) and group identity (random) as parameters. However, having done some more reading in the last couple of days I suspect that I am wrong here and need to use a generalized linear mixed model with a logit link function. Is this the case? I'd really like to understand why. Part of my suspicion lies in 1) the response variable being a proportion and thus bound my a minimum of 0.0 and maximum of 1.0, AND/OR 2) the distribution of the response variable is severely non-normal.
 
Perhaps it is prudent to give you a quick run-down of the reason for why I'm analysing these data. The raw data clearly show pronounced temporal variability in the amount of time groups associate with one another, both within and among years.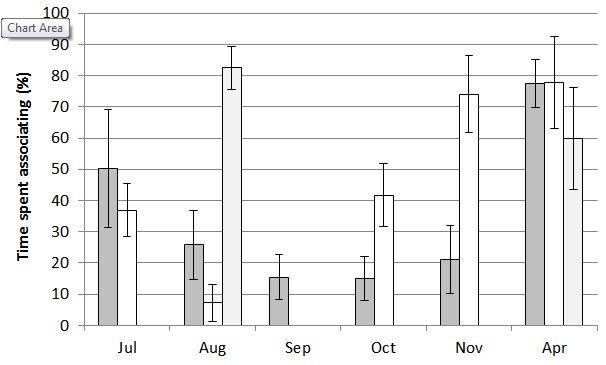


Percentage time groups associated with one another (means with standard error). Column shading indicates the three different years.

My goal with the analysis is simply to support the statement that groups vary in the degree to which they associate with one another within a year, but this variability is not repeatable between years. (I will then argue this is coincident with intra- and inter-annual variability in breeding activity, such that when groups are breeding they associate less frequently).

Thank you again for the taking the time to consider my problem and providing advice.

Cheers,
Dean

[Maguin, Eugene]

I just looked at your capture file and while I certainly don't understand your project, it looks like the species/animals/groups, whatever they are either interact or they don't. About 52% is 0-5 and about 25% is 95-100. I don't know what the x-axis numbers represent but it seems to me that there are three groups: 0-5=None, 6-94=Some, 95-100=All. This characterization of the data may absolutely not fit with the project's aims or data conceptualization within your field. If it did, you could use either a nominal multinomial or an ordinal multinomial distribution function.
Gene Maguin


-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of DP_Sydney
Sent: Friday, July 24, 2015 2:14 AM
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

Hi Rich and Bruce,

Thanks very much for the advice. I have read David Warton's paper (thanks very much for the link Bruce!) and have attempted to digest the issue I am faced with. To me, it doesn't seem like my data conform to a typical 'trials and events' format, but is a binomial proportion as described by Warton and thus a logit transform, as you have both suggested, would be appropriate.
But, I do indeed have a problem with many 0.0 and 1.0 proportions in my
dataset:
<http://spssx-discussion.1045642.n5.nabble.com/file/n5730277/Capture.jpg>

I like the idea of using an adjusted proportion so I can apply a logit transformation. Rich, could you please confirm that the adjustment needs to be made to ALL values, not just values of 0.0 and 1.0?

From there, I originally expected I could run an 'ANOVA-type' general linear mixed model with month (fixed), year (random) and group identity (random) as parameters. However, having done some more reading in the last couple of days I suspect that I am wrong here and need to use a generalized linear mixed model with a logit link function. *Is this the case?* I'd really like to understand why. Part of my suspicion lies in 1) the response variable being a proportion and thus bound my a minimum of 0.0 and maximum of 1.0, AND/OR 2) the distribution of the response variable is severely non-normal.
 
Perhaps it is prudent to give you a quick run-down of the reason for why I'm analysing these data. The raw data clearly show pronounced temporal variability in the amount of time groups associate with one another, both within and among years.
<http://spssx-discussion.1045642.n5.nabble.com/file/n5730277/Capture3.jpg>
My goal with the analysis is simply to support the statement that groups vary in the degree to which they associate with one another within a year, but this variability is not repeatable between years. (I will then argue this is coincident with intra- and inter-annual variability in breeding activity, such that when groups are breeding they associate less frequently).

Thank you again for the taking the time to consider my problem and providing advice.

Cheers,
Dean



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730277.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Rich Ulrich]

I've got some important comments, down below the couple of lines I quote.

> Date: Thu, 23 Jul 2015 23:13:51 -0700
> From: [hidden email]
> Subject: Re: General Linear Model using proportions as raw data - transformation needed?
> To: [hidden email]
>
> Hi Rich and Bruce,
>
...
> But, I do indeed have a problem with many 0.0 and 1.0 proportions in my
> dataset:
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5730277/Capture.jpg>

Over-dispersed!

>
> I like the idea of using an adjusted proportion so I can apply a logit
> transformation. Rich, could you please confirm that the adjustment needs to
> be made to ALL values, not just values of 0.0 and 1.0?

For data with unequal observation times, I think adjusting just 0 and 1 would
not work well.  "The proof of the pudding is in the eating."  Do you like the
"scaling" that will result?   I have done adjustments to only the extreme value
when the biological measuring tool has a minimum for accurate recording.
For instance, if the smallest good value is 0.01, I could use 0.005 to estimate
the biological value to replace (the probably impossible) recorded value of 0.

I looked at the chart that shows distribution of scores.  If you see no value in
separating out 0 and 100 from their respective categories, the problem goes away
if you start with these ranges: Use the mid-point of each range as the proportion.

However.
Gene points to your vast amount of over-dispersion, with your chart showing
75% of cases in the extreme categories of 0-5 or 95-100.  I wonder, how many non-
zero event-counts are in the 0-5 range?  Is there distinction between 1 and 2 as the
scores, before creating the proportion?

Modeling over-dispersion for the Poisson is common.  Mathematically, it effectively
uses a dummy parameter to separate out the effect of Zero, then models Poisson
on the shape of the rest of the data.  I assume that modeling over-dispersion for
Binomial (Google shows some hits) will, in effect, use two dummies to take out the
extremes.  The question you must ask yourself is whether there is enough useful
information left over -- for this dataset -- to get extra meaning from the variation in
the scores in the middle.  Gene's suggestion, use (very little, some, almost all) implies
that the answer is No, that your interesting variation and variance is accounted-for
by the extremes. 

I tend to agree with Gene for these data, except that I would want to ask you whether
(0-5) is good, or should "0" be separated out? (...similarly for "100").  In my experience,
0 (or 100) is sometimes special enough -- logically, before doing statistical tests -- that
I would consider, for your data, something like (0, very little, some, almost all, all): 
This is an ordinal scale.  What you want is something that is at least ordinal, with boundaries
so that it tends toward "equal interval" when it comes to explanations of the hypothesis. 
That is "The proof of the pudding" when it comes to deciding on transformations. 

"Equal interval" for scores for the predictor is not determined by the data collection, but
by the expected effect on the outcome.  "Equal interval" for the outcome is determined by
our interest in drawing distinctions.  - And, testing gets awkward (to say the least) whenever
the equal intervals do not correspond to homogeneous variances across the range of scores. 

--
Rich Ulrich

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[DP_Sydney]

Hi,

I gather the over-dispersion renders using a Generalised Linear Mixed Model with logit-link function on transformed proportions inappropriate, though I would really appreciate confirmation that I was on the right track IF the data were not over-dispersed. Thoughts?

Rich, to answer your questions. Only three values in the 0-5 range were >0.0. I don't understand what you mean by "Is there distinction between 1 and 2 as the scores, before creating the proportion?" What is "1 and 2"?

Gene makes a very good point that, for the most part, groups are either alone or together during the time they are observed.

HOW TO PROCEED?

OPTION 1) Based on Rich's and Gene's comments, convert the proportions to an ordinal variable: 1 ( 0.0%), 2 (>0.0% – 33.3%), 3 (>33.3% – 66.7%), 4 (>66.7% - 99.9%), 5 (100.0%).
I have never analysed ordinal variables before, so how would I go about analysis? Gene mentioned using an ordinal multinomial distribution function, but in what sort of analysis?

OPTION 2) Reduce the observation sessions/visits to a binomial variable based on the status at the onset of the session. That is, 0 = alone, 1 = present. (This would increase my sample size since I had excluded sessions <30 minutes). Rich, I only partially followed your discussion of equal interval. Is my proposed ordinal scale suitable?
I have only analysed binomial variables using logistic regression (i.e. continuous predictor), so I'm unsure how to go about running an analysis with categorical predictors (i.e. year, month, year*month, group identity). Thoughts?

I'm keen to find the simplest option as I am really only interested in "stating the obvious" with some statistical support: association between groups varies within a year and among years.

I very much appreciate all the comments from everyone who has replied to this thread. I have learned much more about handling proportions that I'm sure will come in handy in the future.

Cheers,
Dean

[Maguin, Eugene]

I'd like to reply to just this question/comment.
>> OPTION 1) Based on Rich's and Gene's comments, convert the proportions to an ordinal variable: 1 ( 0.0%), 2 (>0.0% – 33.3%), 3 (>33.3% – 66.7%), 4 (>66.7% - 99.9%), 5 (100.0%).
I have never analyzed ordinal variables before, so /how would I go about analysis?/ Gene mentioned using an ordinal multinomial distribution function, but in /what sort of analysis?/

What I was getting at is this. Suppose you have a DV with three or more categories and an IV. So far as I know you have two choices for the IV-DV relationship. An ordinal relationship assumes that the IV (slope) coefficients are not different across levels of the DV. I haven't checked before saying this but I think that only the (old) PLUM command includes a test  for homogeneity of slopes. (I think that the omission of this test is an important limitation of the Genlin and Genlinmixed commands.) The alternative is a "by-category" relationships (I'm sure there is a better word, sorry.) Essentially, this is a set of (binary) logistic regressions comparing all pairs of categories. So, the IV coefficient for category 2 vs 1 may be marked different from that for category 3 vs 1 or for category 3 vs 2. This analysis can be done using the (old) NOMREG commands as well as (I think, haven't checked) Genlin and Genlinmixed.
A reference is J. S. Long, "Regression models for categorical and limited dependent variables". But, I'll bet that there are similar references from people in your area, which must be biology or ecology given your topic.

If you step back, the problem you have is how model a bimodal distribution. I'd be interested hear about the alternatives from an expert on these types of data.

Gene Maguin



-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of DP_Sydney
Sent: Sunday, July 26, 2015 1:21 AM
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

Hi,

I gather the over-dispersion renders using a Generalised Linear Mixed Model with logit-link function on transformed proportions inappropriate, though I would really appreciate confirmation that I was on the right track IF the data were not over-dispersed. /Thoughts?/

Rich, to answer your questions. Only three values in the 0-5 range were
>0.0. I don't understand what you mean by "Is there distinction between
>1
and 2 as the scores, before creating the proportion?" /What is "1 and 2"?/

Gene makes a very good point that, for the most part, groups are either alone or together during the time they are observed.

*HOW TO PROCEED?*

OPTION 1) Based on Rich's and Gene's comments, convert the proportions to an ordinal variable: 1 ( 0.0%), 2 (>0.0% – 33.3%), 3 (>33.3% – 66.7%), 4 (>66.7% - 99.9%), 5 (100.0%).
I have never analysed ordinal variables before, so /how would I go about analysis?/ Gene mentioned using an ordinal multinomial distribution function, but in /what sort of analysis?/

OPTION 2) Reduce the observation sessions/visits to a binomial variable based on the status at the onset of the session. That is, 0 = alone, 1 = present. (This would increase my sample size since I had excluded sessions
<30 minutes). Rich, I only partially followed your discussion of equal interval. Is my proposed ordinal scale suitable?
I have only analysed binomial variables using logistic regression (i.e.
continuous predictor), so I'm unsure how to go about running an analysis with categorical predictors (i.e. year, month, year*month, group identity).
/Thoughts?/

I'm keen to find the simplest option as I am really only interested in "stating the obvious" with some statistical support: association between groups varies within a year and among years.

I very much appreciate all the comments from everyone who has replied to this thread. I have learned much more about handling proportions that I'm sure will come in handy in the future.

Cheers,
Dean



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730290.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Maguin, Eugene]

I was reading how a given distribution can be approximated by a mixture of distributions. Maybe this will be a useless suggestion but I suggest you see what the literature in your area says about 'mixture models' and if there is anybody there that knows about these models. Let me add that if this is a useful thing, it cannot be done in spss as a defined command but maybe using an R routine. Also perhaps sas or stata but I really don't know about them.
Best wishes, Gene Maguin


-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of DP_Sydney
Sent: Sunday, July 26, 2015 1:21 AM
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

Hi,

I gather the over-dispersion renders using a Generalised Linear Mixed Model with logit-link function on transformed proportions inappropriate, though I would really appreciate confirmation that I was on the right track IF the data were not over-dispersed. /Thoughts?/

Rich, to answer your questions. Only three values in the 0-5 range were
>0.0. I don't understand what you mean by "Is there distinction between
>1
and 2 as the scores, before creating the proportion?" /What is "1 and 2"?/

Gene makes a very good point that, for the most part, groups are either alone or together during the time they are observed.

*HOW TO PROCEED?*

OPTION 1) Based on Rich's and Gene's comments, convert the proportions to an ordinal variable: 1 ( 0.0%), 2 (>0.0% – 33.3%), 3 (>33.3% – 66.7%), 4 (>66.7% - 99.9%), 5 (100.0%).
I have never analysed ordinal variables before, so /how would I go about analysis?/ Gene mentioned using an ordinal multinomial distribution function, but in /what sort of analysis?/

OPTION 2) Reduce the observation sessions/visits to a binomial variable based on the status at the onset of the session. That is, 0 = alone, 1 = present. (This would increase my sample size since I had excluded sessions
<30 minutes). Rich, I only partially followed your discussion of equal interval. Is my proposed ordinal scale suitable?
I have only analysed binomial variables using logistic regression (i.e.
continuous predictor), so I'm unsure how to go about running an analysis with categorical predictors (i.e. year, month, year*month, group identity).
/Thoughts?/

I'm keen to find the simplest option as I am really only interested in "stating the obvious" with some statistical support: association between groups varies within a year and among years.

I very much appreciate all the comments from everyone who has replied to this thread. I have learned much more about handling proportions that I'm sure will come in handy in the future.

Cheers,
Dean



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730290.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Rich Ulrich]

In regards to the questions addressed to me --

My thought about the 0-5% range:  You computed proportion as 0, 1, 2, 3... 
divided by Minutes that might be from 30 to 300.   1/30 is less than 5%; 2/30 is not.
From your reply, the modes of the un-grouped percentage are 0 and 100; and everything
between 0 and 100 is relatively flat, whether you look at percentage or actual numerator.
There is nothing special about 1 "event"; it is not a third mode, after 0 and [all].

Your proposed "ordinal scale"  looks okay -- If it is not equal-interval, it ought to
be close enough to it that you should expect some gain in power from using it.
My intent is always to form "ordinal" that is close to equal-interval; I do not want
the extra d.f.  that are entailed by keeping them discrete, since that weakens both
the testing and the conclusions. 

On the other hand, if you want the simple, definite statement, you may be better off
using your dichotomy, 0 vs 1 (either All, or Start). 

One problem with modeling as a Log-Linear Model, using (0,1), group, Year, Month,
and Year*Month    is that there are 12 months, and so this model has MANY degrees
of freedom.  I think I would look at the data for Months, ignoring year and group, and
create 3 or 4 Seasons.  - That, however, might not be sensitive to a slight shift in
timing, if that is what you were expecting.  That would call for some sort of time-series
analysis.  If someone mentioned "time series",  I did not note it.  Would that be
a good possibility?

--
Rich Ulrich

> Date: Sat, 25 Jul 2015 22:20:33 -0700

> From: [hidden email]
> Subject: Re: General Linear Model using proportions as raw data - transformation needed?
> To: [hidden email]
>
> Hi,
>
> I gather the over-dispersion renders using a Generalised Linear Mixed Model
> with logit-link function on transformed proportions inappropriate, though I
> would really appreciate confirmation that I was on the right track IF the
> data were not over-dispersed. /Thoughts?/
>
> Rich, to answer your questions. Only three values in the 0-5 range were
> >0.0. I don't understand what you mean by "Is there distinction between 1
> and 2 as the scores, before creating the proportion?" /What is "1 and 2"?/
>
> Gene makes a very good point that, for the most part, groups are either
> alone or together during the time they are observed.
>
> *HOW TO PROCEED?*
>
> OPTION 1) Based on Rich's and Gene's comments, convert the proportions to an
> ordinal variable: 1 ( 0.0%), 2 (>0.0% – 33.3%), 3 (>33.3% – 66.7%), 4
> (>66.7% - 99.9%), 5 (100.0%).
> I have never analysed ordinal variables before, so /how would I go about
> analysis?/ Gene mentioned using an ordinal multinomial distribution
> function, but in /what sort of analysis?/
>
> OPTION 2) Reduce the observation sessions/visits to a binomial variable
> based on the status at the onset of the session. That is, 0 = alone, 1 =
> present. (This would increase my sample size since I had excluded sessions
> <30 minutes). Rich, I only partially followed your discussion of equal
> interval. Is my proposed ordinal scale suitable?
> I have only analysed binomial variables using logistic regression (i.e.
> continuous predictor), so I'm unsure how to go about running an analysis
> with categorical predictors (i.e. year, month, year*month, group identity).
> /Thoughts?/
>
> I'm keen to find the simplest option as I am really only interested in
> "stating the obvious" with some statistical support: association between
> groups varies within a year and among years.
>
> I very much appreciate all the comments from everyone who has replied to
> this thread. I have learned much more about handling proportions that I'm
> sure will come in handy in the future.
>

...

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[DP_Sydney]

Hi Rich and Gene,

Thanks for keeping the comments coming. I have reached one conclusion from this discussion: I am out of my depth with analysing these data. But, I will attempt to put together a plan to analyse these data.

I gather that there isn't much of a difference between using the ordinal probabilities approach (i.e. 0, 0.1-33.3, 33.4-66.7, 66.8-99.9, 1.00) vs binomial (0 = alone, 1 = together) approach. The analysis would still be a log-linear model with group ID, month, year, and month*year as parameters using either Regression->Ordinal or Regression->Binary Logistic procedures in SPSS. Am I correct?

Rich, you make the comment that the number of months would substantially increase the DF. I don't follow why this is an issue and my reading of ordinal regression since your post hasn't clarified it at all for me. Also note, that there are only 6 months with data for both Year 1 and Year 2 (Jul, Aug, Sep, Oct, Nov, Apr) with Year 3 having only two months in common (Aug, Apr). At this stage, I'm happy to ignore Year 3 as this greatly complicates the analysis (though perhaps I could add on two additional analyses, one for August comparing years, and another for April comparing years?).

Am I on the right track?

BTW I think time-series analysis is too sophisticated for the goal of my analysis, which is simply to support the temporal variability evident in the raw data. The results of the analysis will literally appear as one or two sentences in the discussion of the paper I am writing, along the lines of "The time groups spent associating with one another was temporally unpredictable, varying considerably during the course of the year and between years". This is quite simple and vague, but delving further into the data provides little information that would be of further biological significance.

Thanks again!
Dean

Thanks again,
Dean

[Rich Ulrich]

"Increase in the d.f."  is important.  It is easier to describe in the sums-of-squares
test than in the maximum likelihood test, but the principle works out exactly the same.

Look at the F-test: Mean-square hypothesis divided by Mean-square error.   (MSh/MSe).
Equivalently, that is Sum-of-squares/d.f.H   divided by Sum-of-squares/d.f.e .  

From inspection of the formula:  You get a bigger (more powerful) F  if the same SSh
is divided by a smaller d.f.   Now, IF those months that you are combining are similar
in outcome, THEN the SSh will be practically the same for the 1 d.f.  test as for the many-d.f.
test; therefore, the MSh will be much larger.  THEN, the 1 d.f.  test will be (much) more
powerful in detecting the effect.   Of course, if there is no "effect" present, this does not
create one. 

For 4 or 5 time periods, it is often the case that there will be a linear trend across time.
This came up very commonly in Repeated Measures analysis on clinical data.

I have always looked at those by asking for the linear trend.  The SS can be partitioned into
linear, quadratic, cubic, etc., in order to test each; maybe quadratic could be interesting,
but I usually only looked at the linear vs. non-linear partition.  Often, the SS for Linear
would be upwards of 90% of the total SS between groups; and that is a much more powerful
test than the test across 4 or 5 periods.

Nathan Mantel wrote hundreds of papers showing how various test circumstances could
be reduced to "one 1 d.f.  test  for one hypothesis"; I was suitably impressed.  You waste
power if you test your hypothesis with more than the minimum d.f.   That is one reason
why we generate Scales and composite scores, instead of doing dozens of tests with items. 
Another reason is that if you carefully ask one question, you get only one answer, avoiding
all that "multiple-testing" philosophical discussion.

PS - you have a shorter time series than I thought; and it seems to be interrupted. 
But if you do not have seasonal effects, you seem to have some other variable that
is not accounted for, to explain the 0 vs. 100%  dichotomy of outcomes.

--
Rich Ulrich

> Date: Thu, 30 Jul 2015 00:33:37 -0700

> From: [hidden email]
> Subject: Re: General Linear Model using proportions as raw data - transformation needed?
> To: [hidden email]
>
> Hi Rich and Gene,
>
> Thanks for keeping the comments coming. I have reached one conclusion from
> this discussion: I am out of my depth with analysing these data. But, I will
> attempt to put together a plan to analyse these data.
>
> I gather that there isn't much of a difference between using the ordinal
> probabilities approach (i.e. 0, 0.1-33.3, 33.4-66.7, 66.8-99.9, 1.00) vs
> binomial (0 = alone, 1 = together) approach. The analysis would still be a
> log-linear model with group ID, month, year, and month*year as parameters
> using either /Regression->Ordinal/ or /Regression->Binary Logistic/
> procedures in SPSS. *Am I correct*?
>
> Rich, you make the comment that the number of months would substantially
> increase the DF. I don't follow why this is an issue and my reading of
> ordinal regression since your post hasn't clarified it at all for me. Also
> note, that there are only 6 months with data for both Year 1 and Year 2
> (Jul, Aug, Sep, Oct, Nov, Apr) with Year 3 having only two months in common
> (Aug, Apr). At this stage, I'm happy to ignore Year 3 as this greatly
> complicates the analysis (though perhaps I could add on two additional
> analyses, one for August comparing years, and another for April comparing
> years?).
>
> Am I on the right track?
>
> BTW I think time-series analysis is too sophisticated for the goal of my
> analysis, which is simply to support the temporal variability evident in the
> raw data. The results of the analysis will literally appear as one or two
> sentences in the discussion of the paper I am writing, along the lines of
> "The time groups spent associating with one another was temporally
> unpredictable, varying considerably during the course of the year and
> between years". This is quite simple and vague, but delving further into the
> data provides little information that would be of further /biological
> /significance.
>

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Maguin, Eugene]

Could we back up a bit and would you help us understand the procedure-design elements of this project. Fill in the key specific elements of summary sketch in your first post. This request reflects my ignorance of how research is done in your area.

Would you also explain the charts you posted. The "percentage time group associated ..." chart makes sense. Where does the "histogram of raw proportions" come from/how was it computed? That chart is very confusing. I don't know how to put it together with the Percentage time chart.
Gene Maguin



-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of DP_Sydney
Sent: Thursday, July 30, 2015 3:34 AM
To: [hidden email]
Subject: Re: General Linear Model using proportions as raw data - transformation needed?

Hi Rich and Gene,

Thanks for keeping the comments coming. I have reached one conclusion from this discussion: I am out of my depth with analysing these data. But, I will attempt to put together a plan to analyse these data.

I gather that there isn't much of a difference between using the ordinal probabilities approach (i.e. 0, 0.1-33.3, 33.4-66.7, 66.8-99.9, 1.00) vs binomial (0 = alone, 1 = together) approach. The analysis would still be a log-linear model with group ID, month, year, and month*year as parameters using either /Regression->Ordinal/ or /Regression->Binary Logistic/ procedures in SPSS. *Am I correct*?

Rich, you make the comment that the number of months would substantially increase the DF. I don't follow why this is an issue and my reading of ordinal regression since your post hasn't clarified it at all for me. Also note, that there are only 6 months with data for both Year 1 and Year 2 (Jul, Aug, Sep, Oct, Nov, Apr) with Year 3 having only two months in common (Aug, Apr). At this stage, I'm happy to ignore Year 3 as this greatly complicates the analysis (though perhaps I could add on two additional analyses, one for August comparing years, and another for April comparing years?).

Am I on the right track?

BTW I think time-series analysis is too sophisticated for the goal of my analysis, which is simply to support the temporal variability evident in the raw data. The results of the analysis will literally appear as one or two sentences in the discussion of the paper I am writing, along the lines of "The time groups spent associating with one another was temporally unpredictable, varying considerably during the course of the year and between years". This is quite simple and vague, but delving further into the data provides little information that would be of further /biological /significance.

Thanks again!
Dean

Thanks again,
Dean



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/General-Linear-Model-using-proportions-as-raw-data-transformation-needed-tp5730200p5730326.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[DP_Sydney]

Hi Rich and Gene,

Rich, thanks for clarifying your point about degrees of freedom. If I understand this correctly, a high df-error will 'compensate' any inflation in the df-hypothesis (in my case; month and year main effects and month*year interaction term). I have a reasonably high sample size so hopefully this won't be a major issue.

Gene, you asked for a more detailed explanation of the data collection. To summarise:
- Different family groups of animals (n = 24 year 1; n = 21 year 2; n = 17 year 3) were followed for periods ranging from 30 minutes to 6 hours.
- During the observation period the time each group spent alone and the time it spent associating with another family group was recorded. For analysis, the proportion of time the focal group spent associating with another group was used as the dependent (response) variable.
- Observations were carried out in Jul, Aug, Sept, Oct, Nov and Apr of two consecutive years, with observations only in Aug and Apr of the third year. Hence, independent (predictor) variables are month and year, with a month*year interaction term.
- Each family group was observed more than once, but not necessarily in each survey month and some groups were present in only one of the survey years. To control for repeated sampling of family groups and incorporate variability among family groups, group ID needs to be included as a random independent variable.
- Looking at the raw data (ignoring month and year) it is evident that during most of the observation sessions groups were either alone 100% of the observation time or were associating with another group for 100% of the observation time. The histogram is a plot of these raw data (see below), ignoring month and year of collection (i.e. it is a summary of ALL observations pooled), with the horizontal axis indicating the percentage of time a focal group spent associating with another group (grouped into 5% bins for the purposes of graphing).
- The second graph I posted (see below) shows the mean percentage that family groups associated with another family group, separated into month and year. There is clearly a lot of variability both within and between the years.
- The purpose of the data collection was to investigate whether the degree of association between family groups was temporally stable, or whether it varied seasonally (i.e. within a year), and if so, whether this within-year temporal trend was consistent across years. The raw data suggest that there is substantial within-year temporal variation, but this is not consistent between years. As I've said before, the goal with the analysis is very simply to support this general statement.
- This component of my research is a minor one and is not a focus of the paper I am preparing for publication. Indeed, the statement of intra- and inter-annual variability in association between family groups will appear as 1-2 sentences in the discussion.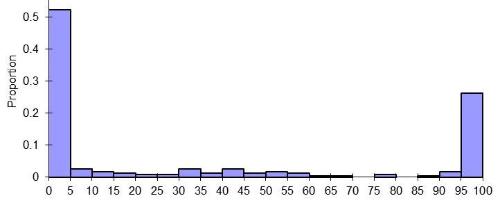


Frequency histogram of raw proportions (i.e. raw data). Y-axis indicates the proportion of all observations collected. X-axis indicates the recorded percentage of time groups associated with one another (i.e. response variable; grouped into 5% bins). The graph shows that most observations involved family groups spending the entire observation time alone (i.e. 0-5% bin along the x-axis) or the entire observation time with another group (i.e. 95-100% bin along the x-axis).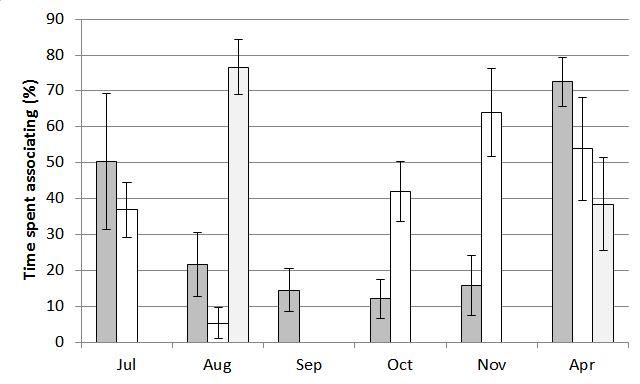


Percentage time groups associating with one another (means with s.e.). Each year is shown as a different shaded column: dark grey = year 1; white = year 2; light grey = year 3 (Aug and Apr only). Means were calculated using all observations recorded in each month/year. (Note all observations in September of Year 2 had a value of 0%).

I hope this makes things clearer. The analysis I am considering is a log-linear model with group ID, month, year, and month*year as parameters using either 'Regression->Ordinal' (if converting the raw proportions into an ordinal scale) or 'Regression->Binary Logistic' (if simplifying each observation session to alone vs together at the onset of the observation session) procedures in SPSS. Does this seem reasonable? 

Cheers,
Dean

PS apologies for the delay in replying (I have been offline).