How do I perform generalized estimating equation for clustered data in SPSS?
How do I perform generalized estimating equation for clustered data in SPSS?
|
Hi everyone,
I am looking at the impact of an intervention on students' knowledge scores (continuous var). - My study has a control group (50 schools) and an intervention group (another 50 schools) which are randomly selected (cluster RCT) from 6 countries. Knowledge scores are reported at baseline and at post-intervention for both intervention and control groups. - Here is my model (standard linear regression): + Dependent var: post-test score + Key independent var: intervention (1) and control (0) + Control vars: gender, country, pre-test score - A similar project said that we need to adjust for the cluster effect. In their project, they said that they use GEE to control for the clustering effect. - I've read about GEE but really can not figure out if I should include "school ID" (100 categories) in the model to control for cluster. If yes, how I can include it in the model? I use SPSS to run the analysis. Any help would be really appreciated. Thanks! |
|
From that description they probably want you to cluster by school in the model. The GENLIN command will look something like:
GENLIN PostScore BY Intervention Gender Country WITH PreScore /MODEL Intervention Gender Country PreScore DISTRIBUTION=NORMAL LINK=IDENTITY /REPEATED SUBJECT=School CORRTYPE=UNSTRUCTURED. Given only 6 countries, I would probably also look at interaction effects for countries, e.g. /MODEL Intervention Country Intervention*Country Gender PreScore and then do an EMMEANS command to get the easier to read contrasts table. |
Re: How do I perform generalized estimating equation for clustered data in SPSS?
|
This post was updated on .
Hi Andy,
Thank you very much for your suggestion. You are truly my lifesaver :D - so I tried both 2 models (Model 1- without interaction term; Model 2- with interaction term) as you suggested. And the coefficients of the key independent (intervention_control group) var change. +The first model gives me a coef of 1.290. +The 2nd model gives me 0.978 I think that the difference is normal because in model 2 I add one more variable to explain the variance of the post-test score. However, how I can figure out which model is better? + In case I should use model 2. How to interpret the interaction term? lets say the coef of Intervention * country 1 = 1.5 (p<0.05). How should I interpret it? + In case I should use model 1 and I want to get the impact of the intervention in each country, what if I split the file by country and get the coef of each country from there? Does it sound good to you? P/S: 2 silly questions: (1) what is the actual role of the Subject and within subject in the "Repeated" section in GEE? What if I entered individual ID variable instead of school ID variable? (2) GEE model itself automatically controls for cluster effect (by selecting "robust estimator"), is it correct? If it's correct, why we need to enter "school" as a repeated subject? I am very new to GEE and there is a lot of confusion for me. Your answer will help me a lot, Thanks a million, |
|
Lot of questions, I will get to the final two as I can kind of answer them quickly.
(1) what is the actual role of the Subject and within subject in the "Repeated" section in GEE? What if I entered individual ID variable instead of school ID variable? This allows the errors in the model between individuals within schools to be correlated with each other. Since you don't have repeated measures for an individual person, if you used as a person ID there is nothing to correlate to. This would make sense if you have multiple test scores per person and stacked the equation (e.g. one for math and one for writing, etc.) (2) GEE model itself automatically controls for cluster effect (by selecting "robust estimator"), is it correct? If it's correct, why we need to enter "school" as a repeated subject? When people say robust it can mean different things. I thought the COV=ROBUST option was for heteroskedastic robust covariance matrices in SPSS. Advocates for GEE say the procedure is generally robust to misspecification of the error covariances as long as the mean equation is correct. So those are two different things. For the others I prefer to just specify the equation at the start I want to sue (I don't put much into the metrics to choose model A over Model B). Given the interaction model is more flexible I would just go with that (if there are no differences it will show). The split file approach has less power than pooling the models (it would be closer to equivalent to having country interaction effects for each right hand side variable), so I wouldn't prefer that either. |
Re: How do I perform generalized estimating equation for clustered data in SPSS?
|
Hi Andy,
I don't know how to say thank you enough. Your short explanation helps me a lot. Thanks again and again and wish you a nice day! Anh |
|
I did a simulation to show how I would do the contrasts for interactions with a binary treatment. It is kind of tricky to get SPSS to do them how I wanted. So here I simulate 3 groups, group 1 the treatment effect is 1.5, groups 2/3 the treatment effect is 0.5.
So you can see in the second GENLIN command is how to get the first order effects in the Estimates table. And then use the COMPARE keyword to test the differences in treatment effects between the groups (the Pairwise Comparisons table). So this does a table for the differences between Group1InterventionEffect - Group2InterventionEffect, Group1InterventionEffect - Group3InterventionEffect, Group2InterventionEffect - Group3InterventionEffect, etc. Unfortunately SPSS shows redundant contrasts, but the final Wald test is the joint test of equality for all 3 tests (with 3 groups there are only 3 independent tests, so it is 2 degrees of freedom for the Chi-square stat). *******************************************************. *Simulated data. DATASET CLOSE ALL. OUTPUT CLOSE ALL. SET SEED 10. INPUT PROGRAM. LOOP Id = 1 TO 10000. END CASE. END LOOP. END FILE. END INPUT PROGRAM. * Intervention variable, need the obverse as well. * To get SPSS to give me the contrast I want. COMPUTE IntV = RV.BERNOULLI(0.5). FORMATS IntV (F1.0). RECODE IntV (1=0)(0=1) INTO NotIntV. * 3 Different group variables. COMPUTE Group = RV.UNIFORM(1,4). COMPUTE Group = TRUNC(Group). FORMATS Group (F1.0). * Now the outcome varies by group. DO IF Group = 1. COMPUTE Y = 0.5 + 0.8 + 1.5*IntV + RV.NORMAL(0,0.1). ELSE IF Group = 2. COMPUTE Y = 0.5 + 0.2 + 0.5*IntV + RV.NORMAL(0,0.1). ELSE IF Group = 3. COMPUTE Y = 0.5 + 0.0 + 0.5*IntV + RV.NORMAL(0,0.1). END IF. EXECUTE. * Here is the typical way people estimate the model and report coeff. * Group 3 is the referent category. GENLIN Y BY Group WITH IntV NotIntV /MODEL Group IntV Group*IntV DISTRIBUTION=NORMAL LINK=IDENTITY /CRITERIA COVB=ROBUST. * Here is how I would do the model to get the contrasts you want. GENLIN Y BY Group WITH IntV NotIntV /MODEL Group*IntV Group*NotIntV DISTRIBUTION=NORMAL LINK=IDENTITY INTERCEPT=NO /CRITERIA COVB=ROBUST /EMMEANS TABLES=Group CONTROL=IntV(1) NotIntV(-1) COMPARE=Group. *******************************************************. 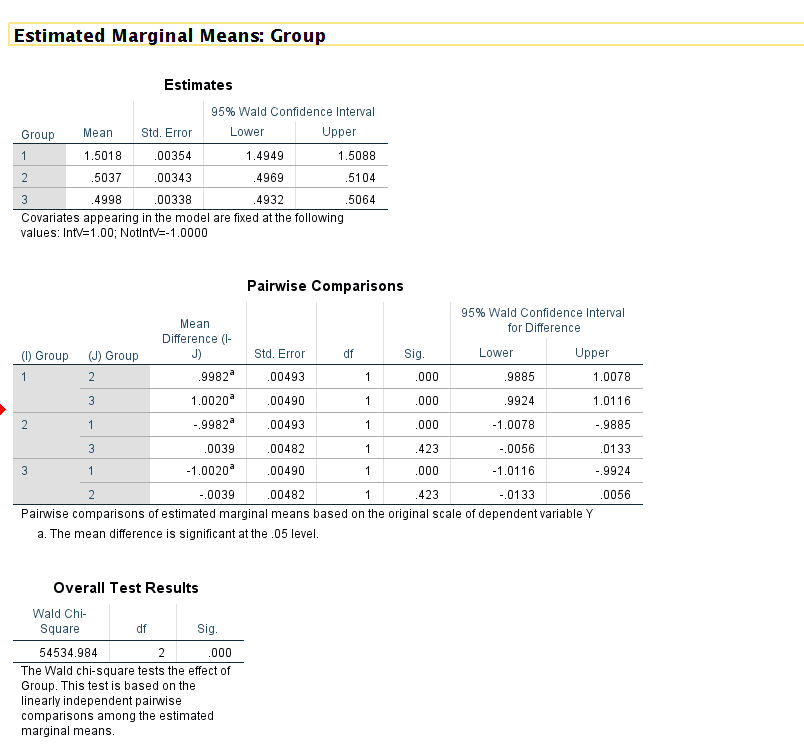
|
Re: How do I perform generalized estimating equation for clustered data in SPSS?
|
Hi Andy,
Thanks so much for your information. I will definitely look into it. I am wondering if there is any way to check if actually students in one cluster are correlated to each other or not. Thank you again and again, Anh |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

