Non-Equivalent Control Groups Design/ Quasi-Experimental Design

[kat92]

Hi,

I would like to know what analysis I should choose to compare the difference between 3 groups. Here's the design: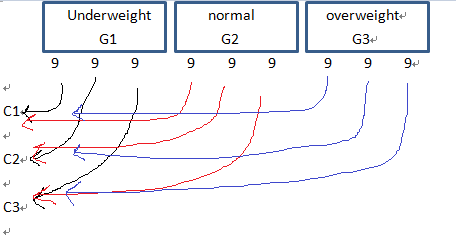



I have 3 conditions (pictures of either underweight, normal weight, or overweight models, as C1, C2, C3), and I assign the participants to each condition according to their own BMI (G1, G2, G3), so that I will make sure there are at least 9 participants in each combination (e.g. C1G1, C1G2, C1G3, C2G1..., a total of 9 combinations). What statistical test should I use if I want to compare the difference between groups in terms of, say body image and weight-loss desire? What method should I choose if I want to control the between-group difference before starting any analysis?

Since the sample size of each group is around 9, is it also a concern for small sample size for running statistics? How can I know how many participants is enough?

Sorry I have a lot of questions in my mind, but I would be really grateful for your answer.

Thanks,
Kat

[David Marso]

You haven't really provided enough information to answer any of these questions.  How for example are "body image" and "weight-loss desire" measured.  VERY IMPORTANT TO KNOW!

"What method should I choose if I want to control the between-group difference before starting any analysis?"  What groups are being compared wrt to what? Between-group difference  in what?  You presumably have heard of random assignment.  Any differences between G1 G2 G3 are obviously not "controllable".  

Re sample size? Good luck on that.  Google Power analysis.  I would suggest consulting with a local statistician or your faculty advisor and experts in the substantive area of research with your measures to get an idea of the general size of mean differences found and the degree of variability within and between groups.

kat92 wrote

Hi,

I would like to know what analysis I should choose to compare the difference between 3 groups. Here's the design:



I have 3 conditions (pictures of either underweight, normal weight, or overweight models, as C1, C2, C3), and I assign the participants to each condition according to their own BMI (G1, G2, G3), so that I will make sure there are at least 9 participants in each combination (e.g. C1G1, C1G2, C1G3, C2G1..., a total of 9 combinations). What statistical test should I use if I want to compare the difference between groups in terms of, say body image and weight-loss desire? What method should I choose if I want to control the between-group difference before starting any analysis?

Since the sample size of each group is around 9, is it also a concern for small sample size for running statistics? How can I know how many participants is enough?

Sorry I have a lot of questions in my mind, but I would be really grateful for your answer.

Thanks,
Kat

[kat92]

Hi David,

Sorry I didn't ask clearly in the previous message. By "body image", I was referring to "body satisfaction". I used Stunkard's Figure Rating Scale before and after the picture-viewing, by asking the participants to choose their current body shape and ideal body shape among the 9 body shapes provided. Therefore, the body image changes is measured by calculating the difference of ideal and current body shape (for pre- and post-test), the greater the difference indicates the greater body dissatisfaction one has. And my hypothesis was that participants (especially those who were overweight) will have lowered body dissatisfaction after viewing pictures of models with similar body shape with them.

"Weight loss desire" is measured as one's ideal weight subtracted by one's current weight. I hypothesized that the participants will have lowered weight loss desire (i.e. smaller difference between ideal weight and current weight in post-test compared to pre-test) after viewing over-weight or normal weight model pictures.

As I did not randomly assign the participants to the groups for picture-viewing (I made sure each picture-viewing condition had equal no. of participants in each BMI classification), I think it should not be considered as random assignment? One of my concerns was that participants in each condition had different level of weight loss desire and body satisfaction due to their own weight. By having 3 conditions (9 participants in each BMI classification x 3 classifications = 27 participants each condition), the difference within and between group might be unpredictable, so I wonder if there's a way to control any (DVs affected by weight).

Thanks!

[kat92]

And one more question, is it correct to perform 3x3 Factorial ANOVA to see if picture-viewing has an effect on their level of body dissatisfaction and weight loss desire?

Thanks a lot!

[Maguin, Eugene]

As I understand your procedure, you have two between factors: model weight category and BMI category. From your reply to David, the dependent variables seem to be "continuous". Computationally, this fits an ANOVA, GLM in spss. I'd say you should be interested in the interaction. You'll get F values and associated p values. Depending on the audience for your work, I think the problem you'll have will be defending your results against alternative explanations such as those David pointed out.
Gene Maguin  

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of kat92
Sent: Thursday, July 14, 2016 5:17 AM
To: [hidden email]
Subject: Re: Non-Equivalent Control Groups Design/ Quasi-Experimental Design

Hi David,

Sorry I didn't ask clearly in the previous message. By "body image", I was referring to "body satisfaction". I used Stunkard's Figure Rating Scale before and after the picture-viewing, by asking the participants to choose their current body shape and ideal body shape among the 9 body shapes provided. Therefore, the body image changes is measured by calculating the difference of ideal and current body shape (for pre- and post-test), the greater the difference indicates the greater body dissatisfaction one has.
And my hypothesis was that participants (especially those who were
overweight) will have lowered body dissatisfaction after viewing pictures of models with similar body shape with them.

"Weight loss desire" is measured as one's ideal weight subtracted by one's current weight. I hypothesized that the participants will have lowered weight loss desire (i.e. smaller difference between ideal weight and current weight in post-test compared to pre-test) after viewing over-weight or normal weight model pictures.

As I did not randomly assign the participants to the groups for picture-viewing (I made sure each picture-viewing condition had equal no. of participants in each BMI classification), I think it should not be considered as random assignment? One of my concerns was that participants in each condition had different level of weight loss desire and body satisfaction due to their own weight. By having 3 conditions (9 participants in each BMI classification x 3 classifications = 27 participants each condition), the difference within and between group might be unpredictable, so I wonder if there's a way to control any (DVs affected by weight).

Thanks!



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Non-Equivalent-Control-Groups-Design-Quasi-Experimental-Design-tp5732723p5732725.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Mike]

From what the OP has said, he *COULD* have a randomized
block (3 levels of BMI as blocks) and with the 2nd independent variable
being the "C" variable (3 levels of pictures) IF he had randomized
the picture conditions within each Block.  Let's think about this
in ANOVA terms:

Main effect of blocks:  because this variable is an attribute
of the subject/participant, differences among the 3 blocks
may or may not be significant but if it is significant, one cannot
explain WHY one has a difference because the three blocks
differ on many background variables (a propensity score analysis
and/or use of additional covariate would be appropriate to better
understand why the differences exist).  IF the people within the
blocks do not represent a random sample that poses the problem
of whom the results apply to.

Main effect of Images ("C"): if subjects within a block were
randomly assigned to one of the three image conditions, then
a significant main effect for images would indicate that the type
of image had an effect on person.  One way to randomize
assignment is within each block assign a subject a unique
number between 1-27 and after assignment, randomly distribute
the 27 numbers among the three image groups, allocating
nine numbers (subjects) per group.  Apparently this was not
done which means that type of image is now confounded with
Block level (and any variables producing differences among
blocks).  If one obtained a significant main effect for type of
image, one would not be able to explain why the differences
occurred because the differences could depend upon many
different causes (randomization would have helped to clear
this up).

Interaction of Block by Image:  it should be clear from the above
that even if one obtained a significant interaction, one would
not be able to explain what it means.

One source on this type of analysis -- along with a worked exampled --
but which has randomized assignment for the variable that is
"image type" above (Edwards uses the letter "B") is the following:

Edwards, A. L. (1968). (3rd Ed)  Experimental design in psychological
research.  See Section 13.8 on pages 260-262.

You can look at more recent books for coverage of this material
but the example by Edwards seems to fit your situation best (but he
does it correctly).  For a more comprehensive review of Randomized
Block designs (including designs where the independent variables
are fixed, random, or a combination), how it compares to Completely
randomized designs, and related issues see chapter 8 "Randomized
Block Designs" in Kirk's 4th edition (2013) text "Experimental
Design".  His Figure 8.1-2 shows how the Sum of Squares are
divided up differently in Randomized Block design versus the
Completely Randomized design.  The key word in both designs
is "randomized" which is what you should have kept in mind
when designing your study.  What texts/sources did you use to
come up with your design and how to implement it?

-Mike Palij
New York University
[hidden email]



----- Original Message -----
From: "Maguin, Eugene" <[hidden email]>
To: <[hidden email]>
Sent: Thursday, July 14, 2016 9:33 AM
Subject: Re: Non-Equivalent Control Groups Design/ Quasi-Experimental
Design


As I understand your procedure, you have two between factors: model
weight category and BMI category. From your reply to David, the
dependent variables seem to be "continuous". Computationally, this fits
an ANOVA, GLM in spss. I'd say you should be interested in the
interaction. You'll get F values and associated p values. Depending on
the audience for your work, I think the problem you'll have will be
defending your results against alternative explanations such as those
David pointed out.
Gene Maguin

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of
kat92
Sent: Thursday, July 14, 2016 5:17 AM
To: [hidden email]
Subject: Re: Non-Equivalent Control Groups Design/ Quasi-Experimental
Design

Hi David,

Sorry I didn't ask clearly in the previous message. By "body image", I
was referring to "body satisfaction". I used Stunkard's Figure Rating
Scale before and after the picture-viewing, by asking the participants
to choose their current body shape and ideal body shape among the 9 body
shapes provided. Therefore, the body image changes is measured by
calculating the difference of ideal and current body shape (for pre- and
post-test), the greater the difference indicates the greater body
dissatisfaction one has.
And my hypothesis was that participants (especially those who were
overweight) will have lowered body dissatisfaction after viewing
pictures of models with similar body shape with them.

"Weight loss desire" is measured as one's ideal weight subtracted by
one's current weight. I hypothesized that the participants will have
lowered weight loss desire (i.e. smaller difference between ideal weight
and current weight in post-test compared to pre-test) after viewing
over-weight or normal weight model pictures.

As I did not randomly assign the participants to the groups for
picture-viewing (I made sure each picture-viewing condition had equal
no. of participants in each BMI classification), I think it should not
be considered as random assignment? One of my concerns was that
participants in each condition had different level of weight loss desire
and body satisfaction due to their own weight. By having 3 conditions (9
participants in each BMI classification x 3 classifications = 27
participants each condition), the difference within and between group
might be unpredictable, so I wonder if there's a way to control any (DVs
affected by weight).

Thanks!

--
View this message in context:
http://spssx-discussion.1045642.n5.nabble.com/Non-Equivalent-Control-Groups-Design-Quasi-Experimental-Design-tp5732723p5732725.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[kat92]

Hi Mike,

Thanks for your reply, it was my final year project and my supervisor suggested the research design. She was out of town so I couldn't reach her, that's why I turned to discussion forum for help. I will definitely read the reference you mentioned and think of ways to improve the design. One last question, is collecting the data again the only way for me now?

Thanks.

[Mike]

If collecting the data is not too difficult, I would suggest
replicating the experiment -- we are talking about N=27,
right?  The key thing would be randomize the people in
the blocks across the images, following the example of
Allan Edwards that I provided earlier.  The analysis would
be rather straightforward from there.  Moreover, you could
compare the results from the first experiment to the second
experiment to see how much of a difference the randomization
makes in the results.

It is possible that a source like Kirk or some other researcher
has analyzed a design like you have now and has figured out
a way to make sense of the data but this will entail a search
of the literature and evaluation of the methods.  This could take
a fair amount of time unless someone knows for sure that there
is (or there is not) another way to analyze the data.

The decision I think you have to make is which of the above
options will take less time to do.

-Mike Palij
New York University
[hidden email]


----- Original Message -----
From: "kat92" <[hidden email]>
To: <[hidden email]>
Sent: Thursday, July 14, 2016 10:51 PM
Subject: Re: Non-Equivalent Control Groups Design/ Quasi-Experimental
Design

> Hi Mike,
>
> Thanks for your reply, it was my final year project and my supervisor
> suggested the research design. She was out of town so I couldn't reach
> her,
> that's why I turned to discussion forum for help. I will definitely
> read the
> reference you mentioned and think of ways to improve the design. One
> last
> question, is collecting the data again the only way for me now?
>
> Thanks.
> View this message in context:
> http://spssx-discussion.1045642.n5.nabble.com/Non-Equivalent-Control-Groups-Design-Quasi-Experimental-Design-tp5732723p5732741.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Bruce Weaver]

The diagram in the original post shows (in an somewhat unconventional way) a 3 (weight groups) x 3 (treatments) table with 9 Ss per cell, so N = 81 in total.  I must confess that I haven't followed this thread that closely, but it seems to me the main question boils down to whether the 27 in each weight group were randomly allocated to the 3 treatments.  

Kat, apologies if I missed this earlier in the thread, but how did you allocate the 27 Ss within each weight group to the three treatments?  

HTH.

Mike wrote

If collecting the data is not too difficult, I would suggest
replicating the experiment -- we are talking about N=27,
right?  The key thing would be randomize the people in
the blocks across the images, following the example of
Allan Edwards that I provided earlier.  The analysis would
be rather straightforward from there.  Moreover, you could
compare the results from the first experiment to the second
experiment to see how much of a difference the randomization
makes in the results.

It is possible that a source like Kirk or some other researcher
has analyzed a design like you have now and has figured out
a way to make sense of the data but this will entail a search
of the literature and evaluation of the methods.  This could take
a fair amount of time unless someone knows for sure that there
is (or there is not) another way to analyze the data.

The decision I think you have to make is which of the above
options will take less time to do.

-Mike Palij
New York University

[Mike]

Not speaking for Kat but the following quote from one of his/her earlier
posts is relevant:

|As I did not randomly assign the participants to the groups for
|picture-viewing (I made sure each picture-viewing condition had
|equal no. of participants in each BMI classification), I think it
should
|not be considered as random assignment?

So, the questions are:

(1) How were subjects assigned to the 3x3=9 combinations.
They can't be assigned to BMI conditions, so random assignment
has to be done at the image viewing conditions.

(2) Bruce is correct and I was wrong in saying below that only
27 subjects were needed because there are 9 subjects (replications)
for each of the 9 cells, so 9x9=81 total subjects.

I took Kat at his word that the subjects were not randomly assigned
but perhaps how subjects were assigned to image conditions should
be made clearer (e.g., first 9 subjects in G1C1, second 9 subjects in
G1C2,
etc., or first subjects in G1C1, second subject in G1C2, etc -- I don't
think
one can reasonably argue that either of these assignments are random).

-Mike Palij
New York University
[hidden email]


----- Original Message -----
From: "Bruce Weaver" <[hidden email]>
To: <[hidden email]>
Sent: Friday, July 15, 2016 8:40 AM
Subject: Re: Non-Equivalent Control Groups Design/ Quasi-Experimental
Design

> The diagram in the original post shows (in an somewhat unconventional
> way) a
> 3 (weight groups) x 3 (treatments) table with 9 Ss per cell, so N = 81
> in
> total.  I must confess that I haven't followed this thread that
> closely, but
> it seems to me the main question boils down to whether the 27 in each
> weight
> group were randomly allocated to the 3 treatments.
>
> Kat, apologies if I missed this earlier in the thread, but how did you
> allocate the 27 Ss within each weight group to the three treatments?
>
> HTH.
>
>
>
> Mike wrote
>> If collecting the data is not too difficult, I would suggest
>> replicating the experiment -- we are talking about N=27,
>> right?  The key thing would be randomize the people in
>> the blocks across the images, following the example of
>> Allan Edwards that I provided earlier.  The analysis would
>> be rather straightforward from there.  Moreover, you could
>> compare the results from the first experiment to the second
>> experiment to see how much of a difference the randomization
>> makes in the results.
>>
>> It is possible that a source like Kirk or some other researcher
>> has analyzed a design like you have now and has figured out
>> a way to make sense of the data but this will entail a search
>> of the literature and evaluation of the methods.  This could take
>> a fair amount of time unless someone knows for sure that there
>> is (or there is not) another way to analyze the data.
>>
>> The decision I think you have to make is which of the above
>> options will take less time to do.
>>
>> -Mike Palij
>> New York University
>
>
>
>
>
> -----
> --
> Bruce Weaver
> [hidden email]
> http://sites.google.com/a/lakeheadu.ca/bweaver/
>
> "When all else fails, RTFM."
>
> NOTE: My Hotmail account is not monitored regularly.
> To send me an e-mail, please use the address shown above.
>
> --
> View this message in context:
> http://spssx-discussion.1045642.n5.nabble.com/Non-Equivalent-Control-Groups-Design-Quasi-Experimental-Design-tp5732723p5732745.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.
>
> =====================
> To manage your subscription to SPSSX-L, send a message to
> [hidden email] (not to SPSSX-L), with no body text except
> the
> command. To leave the list, send the command
> SIGNOFF SPSSX-L
> For a list of commands to manage subscriptions, send the command
> INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[kat92]

Hi all,

Yes, there are a total of 81 participants in my study, and 9 subjects in 9 cells. I collected the data online, first by asking their weight and height (to obtain their BMI), then they were asked to randomly click one of the links to either picture-viewing condition. Using the example I made earlier, 3 conditions (C1, C2, C3) and 3 BMI groups (G1, G2, G3), suppose C1 already has 9 subjects from G1, the remaining subjects from G1 will be assigned to C2 or C3 randomly.

I'm not sure if I can still call it random assignment, as I made sure the numbers of each cell were about 9 subjects, with similar no. of subjects from each BMI classification in every condition.

Sorry I didn't provide clear enough information about assignment of subjects, thank you all for your help.