Ordinal Regression: Test of Parallel Lines

[Lotte]

Hi, I am trying to fit a model by using ordinal regression. I have got two co-variates, and one factor with four groups. The dependent variable has 28 points (1.00, 1.25, 1.50... 7) I use SPSS. My research model fits nicely and the sig. of the Parameter Estimates of the IVs are quite good. But; The Sig. of the Test of Parallel Lines is .000. See picture: 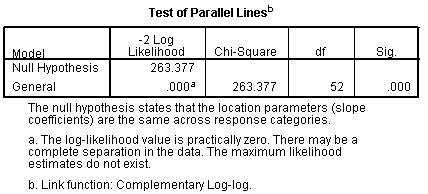The Link Function I use is Complementary log-log. When I switch the Link Function to Probit and Negative log-log, my Test of Parallel Lines is fine, but the model don't fit any more. I have tried regrouping the factors and redusing the number of desimals in the DV to the nearest half (1.00, 1.50, 2.00 ...7). Is there something else I can do, and how can I approach this a little more systematic? Lotte (I'll be only to happy to send all test data if wanted)

[Art Kendall]

Please describe the nature of your DV more fully.  What is the rationale for treating it as ordinal?

Which procedure did you use?

What is your understanding of what kind of problems to use the different links for?

Art Kendall
Social Research Consultants



On 8/26/2010 7:57 PM, Lotte wrote:

Hi, I am trying to fit a model by using ordinal regression. I have got two co-variates, and one factor with four groups. The dependent variable has 28 points (1.00, 1.25, 1.50... 7) I use SPSS. My research model fits nicely and the sig. of the Parameter Estimates of the IVs are quite good. But; The Sig. of the Test of Parallel Lines is .000. See picture: The Link Function I use is Complementary log-log. When I switch the Link Function to Probit and Negative log-log, my Test of Parallel Lines is fine, but the model don't fit any more. I have tried regrouping the factors and redusing the number of desimals in the DV to the nearest half (1.00, 1.50, 2.00 ...7). Is there something else I can do, and how can I approach this a little more systematic? Lotte (I'll be only to happy to send all test data if wanted)

---

View this message in context: Ordinal Regression: Test of Parallel Lines
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Lotte]

Hi, my rational for using ordinal regression is that there is not a linear relationship between DV and IV and the dist ributions are homoskedastic and not normal. And ordinal regression only need 5 cases per IV. I have a small sample (n=60) and I am trying to detect relatively small effects. I am testing a model where I am comparing four groups from an experiment. I also have three covariates. The DV is an average of four items measuring the same construct on a 7-point likert scale [ DV = ( V1 + V2 + V3 + V4 ) /4 ]. The DV is an evaluation of the features of a product. My understanding of which Link Funtion to use is rather weak. I just tried them all until I found one that gave me some results. Prosedure: I don't know. I don't even understand the question. I just used the SPSS strait forward method. New development: I managed to pass the Test for Parallel Lines by rounding of the DV to the next whole digit. The scale is now a 7-point scale [ (1, 2, 3, 4, 5, 6, 7) instead on (1, 1.25, 1.5, 1.75....etc) ]. I first tried rounding of to the nearest half number, but that didn't work. The new problem is that the sig. of parameter estimates for the IV is not as good. So new question: Can I somehow rescale the DV so that it meets the Test of Parallel Lines, but still remains more of its sensitivity? All the best, Lotte PS: I can send you the output in a jpg file if you are interested.

[Art Kendall]

Please describe your 4 groups. 4  treatments? pre-test/post-test by experiment/control? 4 doses of 1 treatment?

What is the measurement of your covariates?

Why would homoskedasticity be a problem?

What distributions are not normal?

Your syntax should name the procedure.  (if you are using the GUI, exit via <paste>.)

How did the reliability of the DV measure look?


Art Kendall
Social research Consultants



On 8/27/2010 9:35 AM, Lotte wrote:

Hi, my rational for using ordinal regression is that there is not a linear relationship between DV and IV and the dist ributions are homoskedastic and not normal. And ordinal regression only need 5 cases per IV. I have a small sample (n=60) and I am trying to detect relatively small effects. I am testing a model where I am comparing four groups from an experiment. I also have three covariates. The DV is an average of four items measuring the same construct on a 7-point likert scale [ DV = ( V1 + V2 + V3 + V4 ) /4 ]. The DV is an evaluation of the features of a product. My understanding of which Link Funtion to use is rather weak. I just tried them all until I found one that gave me some results. Prosedure: I don't know. I don't even understand the question. I just used the SPSS strait forward method. New development: I managed to pass the Test for Parallel Lines by rounding of the DV to the next whole digit. The scale is now a 7-point scale [ (1, 2, 3, 4, 5, 6, 7) instead on (1, 1.25, 1.5, 1.75....etc) ]. I first tried rounding of to the nearest half number, but that didn't work. The new problem is that the sig. of parameter estimates for the IV is not as good. So new question: Can I somehow rescale the DV so that it meets the Test of Parallel Lines, but still remains more of its sensitivity? All the best, Lotte PS: I can send you the output in a jpg file if you are interested.

---

View this message in context: Re: Ordinal Regression: Test of Parallel Lines
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Art Kendall]

The second question should be
What is the measurement level of your covariates?

On 8/27/2010 10:54 AM, Art Kendall wrote:

Please describe your 4 groups. 4  treatments? pre-test/post-test by experiment/control? 4 doses of 1 treatment?

What is the measurement of your covariates?

Why would homoskedasticity be a problem?

What distributions are not normal?

Your syntax should name the procedure.  (if you are using the GUI, exit via <paste>.)

How did the reliability of the DV measure look?


Art Kendall
Social research Consultants



On 8/27/2010 9:35 AM, Lotte wrote:

Hi, my rational for using ordinal regression is that there is not a linear relationship between DV and IV and the dist ributions are homoskedastic and not normal. And ordinal regression only need 5 cases per IV. I have a small sample (n=60) and I am trying to detect relatively small effects. I am testing a model where I am comparing four groups from an experiment. I also have three covariates. The DV is an average of four items measuring the same construct on a 7-point likert scale [ DV = ( V1 + V2 + V3 + V4 ) /4 ]. The DV is an evaluation of the features of a product. My understanding of which Link Funtion to use is rather weak. I just tried them all until I found one that gave me some results. Prosedure: I don't know. I don't even understand the question. I just used the SPSS strait forward method. New development: I managed to pass the Test for Parallel Lines by rounding of the DV to the next whole digit. The scale is now a 7-point scale [ (1, 2, 3, 4, 5, 6, 7) instead on (1, 1.25, 1.5, 1.75....etc) ]. I first tried rounding of to the nearest half number, but that didn't work. The new problem is that the sig. of parameter estimates for the IV is not as good. So new question: Can I somehow rescale the DV so that it meets the Test of Parallel Lines, but still remains more of its sensitivity? All the best, Lotte PS: I can send you the output in a jpg file if you are interested.

---

View this message in context: Re: Ordinal Regression: Test of Parallel Lines
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Lotte]

Hi again,

its a 2x2 experiment which gives four conditions. No crontrol group.

The DV is not normal, also if I look at the distribution by group.
Two of the co-variates are normal, also within each group.

The covariates are also an average of six items. So the scale is, well, I suppose 6*7=42.
I should probably round of these too.

Syntax: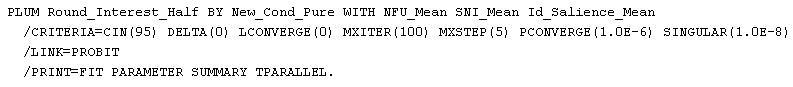


The DV's Cronbach's Alpha is 0.893

Lotte :-)

[Ling Ting]

I am out of the office from 12:30  to 5pm on August 27.   If you need immediate assistance please contact 479-575-2905.  Thank you.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Art Kendall]

  In applications of the general linear model, it is irrelevant what the
distribution of the raw data looks like.  What is important is that the
residuals ("errors") be not blatantly discrepant from normal.

When people worry about measurement level being interval vs ordinal
level is mostly when there are 3 to five levels for the DV.

Rounding only throws away information.  The ultimate in rounding is to
commit the nefarious median split.

After you do exploratory graphics, I suggest you use the general linear
model, i.e., ANOVA, or REGRESSION, or GLM.


Please clarify your two IVs if this is an _experiment_ and there is no
control group.

If this is unclear or if you wish to see comments by other members of
this list on what I am advising, feel free to post to this list again.

Art Kendall
Social Research Consultants

On 8/27/2010 1:58 PM, Lotte wrote:

> Hi again,
>
> its a 2x2 experiment which gives four conditions. No crontrol group.
>
> The DV is not normal, also if I look at the distribution by group.
> Two of the co-variates are normal, also within each group.
>
> The covariates are also an average of six items. So the scale is, well, I
> suppose 6*7=42.
> I should probably round of these too.
>
> Syntax:
> http://spssx-discussion.1045642.n5.nabble.com/file/n2740387/Syntax.jpg
>
> The DV's Cronbach's Alpha is 0.893
>
> Lotte :-)
>
> --
> View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Ordinal-Regression-Test-of-Parallel-Lines-tp2739362p2740387.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.
>
> =====================
> To manage your subscription to SPSSX-L, send a message to
> [hidden email] (not to SPSSX-L), with no body text except the
> command. To leave the list, send the command
> SIGNOFF SPSSX-L
> For a list of commands to manage subscriptions, send the command
> INFO REFCARD
>

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD