plotdeviance from mean

[francesca]

Hi,

I want to create a plot in SPSS showing each data point plus the mean shown as a line and connected to each data point

This is how does it look like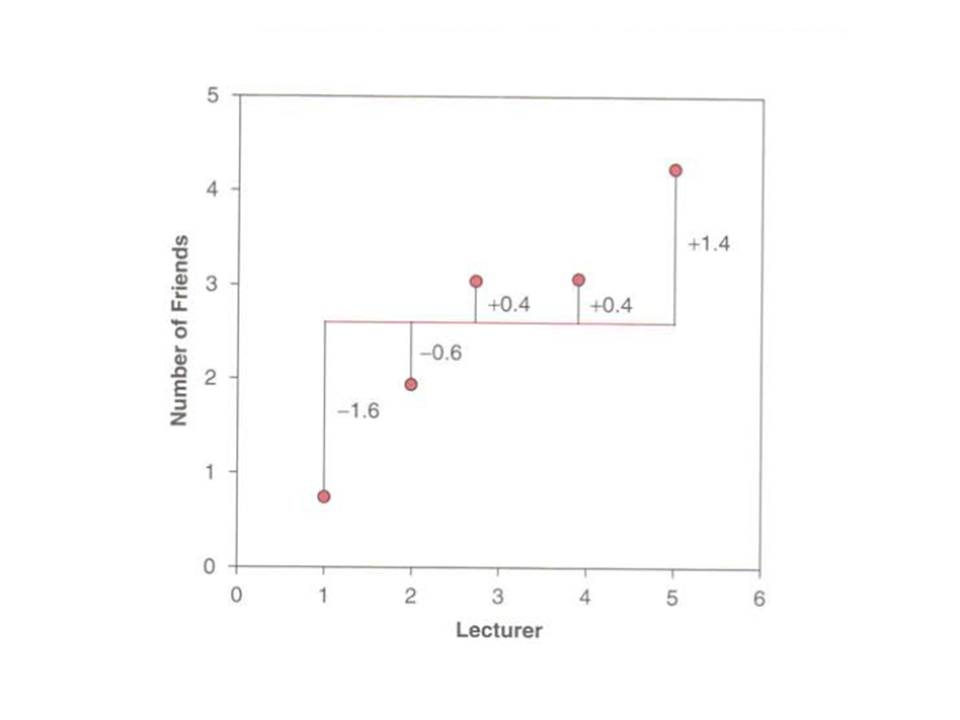



Does anybody know how to make it in SPSS?

It is basically showing a deviance from the mean

Thank you

Francesca

[Andy W]

Here is an example, also see some other related examples on this blog post, https://andrewpwheeler.wordpress.com/2013/06/27/some-discussion-on-circular-helio-bar-charts-2/.

********************************************************.
DATA LIST FREE / Lecturer Friends.
BEGIN DATA
1 0.5
2 2.0
3 3.1
4 3.1
5 4.2
END DATA.
AGGREGATE OUTFILE=* MODE=ADDVARIABLES /BREAK /MeanF = MEAN(Friends).
COMPUTE Dev = Friends - MeanF.
FORMATS Dev (F2.1) Friends MeanF Lecturer (F1.0).

*Now the chart.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Lecturer Friends MeanF Dev
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Lecturer=col(source(s), name("Lecturer"), unit.category())
  DATA: Friends=col(source(s), name("Friends"))
  DATA: MeanF=col(source(s), name("MeanF"))
  DATA: Dev=col(source(s), name("Dev"), unit.category())
  GUIDE: axis(dim(1), label("Lecturer"))
  GUIDE: axis(dim(2), label("Number of Friends"))
  ELEMENT: edge(position(Lecturer*(MeanF+Friends)))
  ELEMENT: line(position(Lecturer*MeanF))
  ELEMENT: point(position(Lecturer*Friends), color.interior(color.red), size(size."10"), label(Dev))
END GPL.
********************************************************.

[francesca]

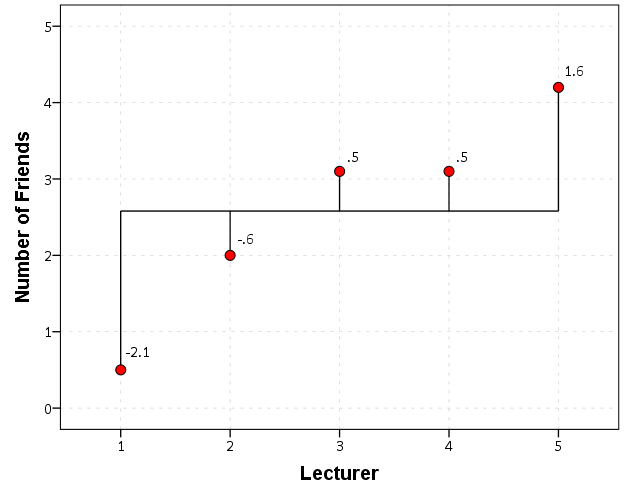
Thank you very much for this.

Unfortunately I don't use the syntax with SPSS. I would just need to know what are the items to select in the list given by the preformed commands on the tools bar.

Thank you

Francesca

2015-03-06 18:11 GMT+00:00 Andy W [via SPSSX Discussion] <[hidden email]>:

Here is an example, also see some other related examples on this blog post, https://andrewpwheeler.wordpress.com/2013/06/27/some-discussion-on-circular-helio-bar-charts-2/.

********************************************************.
DATA LIST FREE / Lecturer Friends.
BEGIN DATA
1 0.5
2 2.0
3 3.1
4 3.1
5 4.2
END DATA.
AGGREGATE OUTFILE=* MODE=ADDVARIABLES /BREAK /MeanF = MEAN(Friends).
COMPUTE Dev = Friends - MeanF.
FORMATS Dev (F2.1) Friends MeanF Lecturer (F1.0).

*Now the chart.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Lecturer Friends MeanF Dev
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Lecturer=col(source(s), name("Lecturer"), unit.category())
  DATA: Friends=col(source(s), name("Friends"))
  DATA: MeanF=col(source(s), name("MeanF"))
  DATA: Dev=col(source(s), name("Dev"), unit.category())
  GUIDE: axis(dim(1), label("Lecturer"))
  GUIDE: axis(dim(2), label("Number of Friends"))
  ELEMENT: edge(position(Lecturer*(MeanF+Friends)))
  ELEMENT: line(position(Lecturer*MeanF))
  ELEMENT: point(position(Lecturer*Friends), color.interior(color.red), size(size."10"), label(Dev))
END GPL.
********************************************************.

Andy W
[hidden email]
http://andrewpwheeler.wordpress.com/

---

If you reply to this email, your message will be added to the discussion below:

http://spssx-discussion.1045642.n5.nabble.com/plotdeviance-from-mean-tp5728900p5728901.html

To unsubscribe from plotdeviance from mean, click here.
NAML

[Andy W]

Sorry I'm pretty sure that chart is not possible with just the GUI. You will need syntax to replicate that chart.

[francesca]

Ok, thank you I will try with the syntax then :)

2015-03-06 18:24 GMT+00:00 Andy W [via SPSSX Discussion] <[hidden email]>:

Sorry I'm pretty sure that chart is not possible with just the GUI. You will need syntax to replicate that chart.

Andy W
[hidden email]
http://andrewpwheeler.wordpress.com/

---

If you reply to this email, your message will be added to the discussion below:

http://spssx-discussion.1045642.n5.nabble.com/plotdeviance-from-mean-tp5728900p5728903.html

To unsubscribe from plotdeviance from mean, click here.
NAML

[John F Hall]

This is exactly the kind of thing I’m looking for to use with my idiosyncratic teaching tool to introduce the idea of regression and correlation using elastic bands, especially if it can be modified to show a vertical line with deviations in addition to the horizontal line, and even better if there were applets available to create an animated version.  Statisticians among you may be horrified, but my (non-numerate) students immediately got the idea and even anticipated the likely end result. 

 

I’ve temporarily uploaded a pdf file to my website which shows what I was trying to do http://surveyresearch.weebly.com/uploads/2/9/9/8/2998485/elastic_bands_(graphic_teaching_aid_for_regression_and_correlation).pdf

I used to have transparencies for use with an O/H projector (epidiascope?) but had to do the graphics in Firefox 10 years ago. 

 

The underlying idea could also be extended to starting with the rigid poles fixed vertically to zero on the X axis and horizontally to the Y axis, then letting go to see where they end up.  I assume they reach the mean of X and Y respectively, with the vertical one representing mean X and a horizontal one mean Y?  If so they could then be pinned through the intersection of mean X and mean Y and allowed to rotate, producing two regression lines, Y on X and X on Y, the cosine of the angle between them being Pearson’s r.

 

Anyway I’d be grateful for any comments on the pedagogy and maths, especially for any syntax to use.  I’ve looked everywhere for applets, but as yet found none that are animated.

 

John F Hall (Mr)

[Retired academic survey researcher]

 

Email:   [hidden email] 

Website: www.surveyresearch.weebly.com

SPSS start page:  www.surveyresearch.weebly.com/1-survey-analysis-workshop

 

 

 

 

 

 

From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of francesca
Sent: 06 March 2015 19:18
To: [hidden email]
Subject: Re: plotdeviance from mean

 

Thank you very much for this.

 

Unfortunately I don't use the syntax with SPSS. I would just need to know what are the items to select in the list given by the preformed commands on the tools bar.

 

Thank you

 

Francesca

 

2015-03-06 18:11 GMT+00:00 Andy W [via SPSSX Discussion] <[hidden email]>:

Here is an example, also see some other related examples on this blog post, https://andrewpwheeler.wordpress.com/2013/06/27/some-discussion-on-circular-helio-bar-charts-2/.

********************************************************.
DATA LIST FREE / Lecturer Friends.
BEGIN DATA
1 0.5
2 2.0
3 3.1
4 3.1
5 4.2
END DATA.
AGGREGATE OUTFILE=* MODE=ADDVARIABLES /BREAK /MeanF = MEAN(Friends).
COMPUTE Dev = Friends - MeanF.
FORMATS Dev (F2.1) Friends MeanF Lecturer (F1.0).

*Now the chart.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Lecturer Friends MeanF Dev
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Lecturer=col(source(s), name("Lecturer"), unit.category())
  DATA: Friends=col(source(s), name("Friends"))
  DATA: MeanF=col(source(s), name("MeanF"))
  DATA: Dev=col(source(s), name("Dev"), unit.category())
  GUIDE: axis(dim(1), label("Lecturer"))
  GUIDE: axis(dim(2), label("Number of Friends"))
  ELEMENT: edge(position(Lecturer*(MeanF+Friends)))
  ELEMENT: line(position(Lecturer*MeanF))
  ELEMENT: point(position(Lecturer*Friends), color.interior(color.red), size(size."10"), label(Dev))
END GPL.
********************************************************.

Andy W
[hidden email]
http://andrewpwheeler.wordpress.com/

 

---

If you reply to this email, your message will be added to the discussion below:

http://spssx-discussion.1045642.n5.nabble.com/plotdeviance-from-mean-tp5728900p5728901.html

To unsubscribe from plotdeviance from mean, click here.
NAML

 

 

---

View this message in context: Re: plotdeviance from mean
Sent from the SPSSX Discussion mailing list archive at Nabble.com.
===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Andy W]

Yes I like the leverage analogy as well, see this cross validated post for some similar graphics, http://stats.stackexchange.com/q/18058/1036.

Another point that helps to see why the board has to rotate around where the two means intersect is that the means on the left hand side have to balance out with the means on the right hand side (for linear equations). E.g.

Y_Mean = Intercept + Slope*(X_Mean)

It always is a bit hand-wavy when trying to get into the nitty gritty of things like squared error, but the leverage analogy and above are pretty simple for undergrads in an intro stats course.

I will work on static graphics to illustrate the lines when I get a chance John. I'm not familiar enough with tools to do the animation (nor with how the animation would work exactly in a lecture).

[John F Hall]

Jignesh

 

Thanks for the compliment!

 

Andy

 

I checked out the link you sent, but my students would be put off by the formulae.

 

Everyone

 

I forgot to say in the document

http://surveyresearch.weebly.com/uploads/2/9/9/8/2998485/elastic_bands_(graphic_teaching_aid_for_regression_and_correlation).pdf

that in class I built up the diagram from scratch using coloured chalk (yes, chalk!) on a chalk-board to draw lines from each point to the mean lines, vertically and horizontally (chalk-dust everywhere).  This helps to explain why negative deviations need to be squared otherwise they just cancel out the positive ones.  Students intuitively understand this. 

 

At the same time as drawing lines on the board, I built up elements of a formula step by step at the other side of the double-width board, starting with the means (and a picture of a see-saw with an elephant on one side and a mouse on the other, the fulcrum being the mean when balance is achieved).  Looking back I should perhaps have made the axes themselves the starting points for the lines (rods), forced them to remain horizontal and vertical, and used the same elastic band analogy to see where they ended up (hopefully the two means).

 

I’ve also just thought of a way to overlay the figures for Y on X and X on Y: if I use MS-Snip to copy/paste the images I might be able to change transparency and move one over the other.  No luck so far.  Tried Google search, Text behind, Text in front, Through etc  but all solutions result in one image blocking view of the other whichever is underneath.  Is there any way to get these images both into the same diagram (using the intersection of the thick red and blue lines to register) ?

 

Thanks for any help.

 

John F Hall (Mr)

[Retired academic survey researcher]

 

Email:   [hidden email] 

Website: www.surveyresearch.weebly.com

SPSS start page:  www.surveyresearch.weebly.com/1-survey-analysis-workshop

 

 

 

 

From: [hidden email] [mailto:[hidden email]] On Behalf Of Jignesh Sutar
Sent: 06 March 2015 20:23
To: John F Hall
Subject: Re: plotdeviance from mean

 

That's a very neat way of explaining a regression line!

 

On 6 March 2015 at 19:13, John F Hall <[hidden email]> wrote:

This is exactly the kind of thing I’m looking for to use with my idiosyncratic teaching tool to introduce the idea of regression and correlation using elastic bands, especially if it can be modified to show a vertical line with deviations in addition to the horizontal line, and even better if there were applets available to create an animated version.  Statisticians among you may be horrified, but my (non-numerate) students immediately got the idea and even anticipated the likely end result. 

 

I’ve temporarily uploaded a pdf file to my website which shows what I was trying to do http://surveyresearch.weebly.com/uploads/2/9/9/8/2998485/elastic_bands_(graphic_teaching_aid_for_regression_and_correlation).pdf

I used to have transparencies for use with an O/H projector (epidiascope?) but had to do the graphics in Firefox 10 years ago. 

 

The underlying idea could also be extended to starting with the rigid poles fixed vertically to zero on the X axis and horizontally to the Y axis, then letting go to see where they end up.  I assume they reach the mean of X and Y respectively, with the vertical one representing mean X and a horizontal one mean Y?  If so they could then be pinned through the intersection of mean X and mean Y and allowed to rotate, producing two regression lines, Y on X and X on Y, the cosine of the angle between them being Pearson’s r.

 

Anyway I’d be grateful for any comments on the pedagogy and maths, especially for any syntax to use.  I’ve looked everywhere for applets, but as yet found none that are animated.

 

John F Hall (Mr)

[Retired academic survey researcher]

 

Email:   [hidden email] 

Website: www.surveyresearch.weebly.com

SPSS start page:  www.surveyresearch.weebly.com/1-survey-analysis-workshop

 

 

 

 

 

 

From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of francesca
Sent: 06 March 2015 19:18
To: [hidden email]
Subject: Re: plotdeviance from mean

 

Thank you very much for this.

 

Unfortunately I don't use the syntax with SPSS. I would just need to know what are the items to select in the list given by the preformed commands on the tools bar.

 

Thank you

 

Francesca

 

2015-03-06 18:11 GMT+00:00 Andy W [via SPSSX Discussion] <[hidden email]>:

Here is an example, also see some other related examples on this blog post, https://andrewpwheeler.wordpress.com/2013/06/27/some-discussion-on-circular-helio-bar-charts-2/.

********************************************************.
DATA LIST FREE / Lecturer Friends.
BEGIN DATA
1 0.5
2 2.0
3 3.1
4 3.1
5 4.2
END DATA.
AGGREGATE OUTFILE=* MODE=ADDVARIABLES /BREAK /MeanF = MEAN(Friends).
COMPUTE Dev = Friends - MeanF.
FORMATS Dev (F2.1) Friends MeanF Lecturer (F1.0).

*Now the chart.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Lecturer Friends MeanF Dev
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Lecturer=col(source(s), name("Lecturer"), unit.category())
  DATA: Friends=col(source(s), name("Friends"))
  DATA: MeanF=col(source(s), name("MeanF"))
  DATA: Dev=col(source(s), name("Dev"), unit.category())
  GUIDE: axis(dim(1), label("Lecturer"))
  GUIDE: axis(dim(2), label("Number of Friends"))
  ELEMENT: edge(position(Lecturer*(MeanF+Friends)))
  ELEMENT: line(position(Lecturer*MeanF))
  ELEMENT: point(position(Lecturer*Friends), color.interior(color.red), size(size."10"), label(Dev))
END GPL.
********************************************************.

Andy W
[hidden email]
http://andrewpwheeler.wordpress.com/

 

---

If you reply to this email, your message will be added to the discussion below:

http://spssx-discussion.1045642.n5.nabble.com/plotdeviance-from-mean-tp5728900p5728901.html

To unsubscribe from plotdeviance from mean, click here.
NAML

 

 

---

View this message in context: Re: plotdeviance from mean
Sent from the SPSSX Discussion mailing list archive at Nabble.com.
===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

 

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Art Kendall]

The use of elastic bands (aka rubber bands) is an excellent way to to show the ideas behind regression.
I am a strong believer in using several different ways to presents concepts.

WRT squaring when dealing with distances, I have found it helpful to start with the Pythagorean theorem in 2 D and then in 3 D.   I only get into squaring distances in 1 D by saying that it is very much the same idea.

I also do a quick demo that the sum of distances of points from the mean based on the first power always comes out as zero.

[John F Hall]

Thanks Art, but someone needs to work out the underlying maths as well.

 

Should have been out in the garden pruning apple trees and preparing vegetable plots, but I've just re-written and uploaded a new version of the document as

4.5.1 Visual aid for regression and correlation:

(http://surveyresearch.weebly.com/uploads/2/9/9/8/2998485/4.5.1_visual_aid_for_regression_and_correlation.pdf)

which includes the overlay of the two regression diagrams, created by my friend Terry Blom using Serif http://www.serif.com/int/fr/freedownloads/desktop-publishing-software/ on his mobile whilst walking the dog!  Needs doing again with a steadier hand, but not bad for what I wanted.

 

Oh for some animated applets!

 

John F Hall (Mr)

[Retired academic survey researcher]

 

Email:   [hidden email] 

Website: www.surveyresearch.weebly.com

SPSS start page:  www.surveyresearch.weebly.com/1-survey-analysis-workshop

 

 

 

 

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of Art Kendall
Sent: 07 March 2015 16:59
To: [hidden email]
Subject: Re: plotdeviance from mean

 

The use of elastic bands (aka rubber bands) is an excellent way to to show the ideas behind regression.

I am a strong believer in using several different ways to presents concepts.

 

WRT squaring when dealing with distances, I have found it helpful to start

with the Pythagorean theorem in 2 D and then in 3 D.   I only get into

squaring distances in 1 D by saying that it is very much the same idea.

 

I also do a quick demo that the sum of distances of points from the mean based on the first power always comes out as zero.

 

 

 

-----

Art Kendall

Social Research Consultants

--

View this message in context: http://spssx-discussion.1045642.n5.nabble.com/plotdeviance-from-mean-tp5728900p5728915.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

 

=====================

To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Art Kendall]

Of course, my message should have been clearer.

I was suggesting supplementing the other ways of teaching math not supplanting them.


Very often student miss the idea that a lot of stat is about describing the distribution of distances between points and summary measures.  In 1 D space, the mean is the calculated point on a distribution that has the smallest average (mean) squared distance from the observed points. The jargon used for this is "least squares". In 2 D, 3 D, etc., regression uses the squared distances along  one of the axes.

They often can relate to 2 D distances, and 3 D distances, and after refreshing that they can more easily relate to using squared distances in 1 D space.

[Rich Ulrich]

Would it help to point out a couple of related generalizations about distances?

 - The median is any value with the smallest average absolute distance to all the points;
 - the mode is any value with the smallest count of values not identical to itself.
For distributions that we wish to presume are symmetrical, the median reduces most
of the influence of a long tail and the mode ignores tails even more thoroughly.


One reason that they are not as useful as the Mean is that there can be two or
more Modes; and the Median, for N divisible by two, will be the whole range
between two non-identical mid-values.

Generalizing otherwise:  The standard deviation is the "root-mean square", that is,
it is the square root of the average of the squared deviations from the mean; we use
that a lot.   The harmonic mean is the reciprocal of the mean of the reciprocals, and
is used implicitly in some ANOVAs.  The geometric mean is the Nth root of the N-fold
product, and students probably heard of it in high school, even if only for two numbers.
The N-fold product is a feature of "likelihood functions", which we ordinarily compute
using the sum of logarithms.

So, yes, statistics does make a lot of use of all the simple ways that you can
manipulate "distances."

--
Rich Ulrich

> Date: Sat, 7 Mar 2015 12:36:55 -0700

> From: [hidden email]
> Subject: Re: plotdeviance from mean
> To: [hidden email]
>
> Of course, my message should have been clearer.
>
> I was suggesting supplementing the other ways of teaching math not
> supplanting them.
>
>
> Very often student miss the idea that a lot of stat is about describing the
> distribution of distances between points and summary measures. In 1 D
> space, the mean is the calculated point on a distribution that has the
> smallest average (mean) squared distance from the observed points. The
> jargon used for this is "least squares". In 2 D, 3 D, etc., regression uses
> the squared distances along one of the axes.
>
> They often can relate to 2 D distances, and 3 D distances, and after
> refreshing that they can more easily relate to using squared distances in 1
> D space.
>

===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

[Andy W]

John,

Here is my general response to the "too many formulae", http://stats.stackexchange.com/a/18094/1036.

At this link is a series of several examples of connecting the lines to demonstrate these concepts, https://dl.dropbox.com/s/t8ddyr3farhvi78/RegLines.sps?dl=0. I leave it to the reader to make more plots of the items superimposed if they wish (the final one in your hand out is a bit busy though in my opinion).

Related, Andrew Gelman had a recent blog post in which he highlighted an online tool where you can move the points and see how the regression line changes, http://andrewgelman.com/2015/03/07/interactive-demonstrations-linear-gaussian-process-regressions/. When you say animations though I'm still not sure what exactly you have in mind.

Andy