Deriving Formula from Ordinal Regression Results to Classify New Cases?

[Vik Rubenfeld]

Very good. Thanks.

[Ryan]

Vik,

I found an example fitting an ordinal logistic regression model using
the PLUM procedure here:

http://www.ats.ucla.edu/stat/SPSS/dae/ologit.htm

The SPSS dataset used for that example is located here:

http://www.ats.ucla.edu/stat/data/ologit.sav

The dependent variable "apply" has three ordered categories (0, 1, and 2).
The independent variables are "pared", "public", and "gpa".

The syntax to fit the model AND obtain the estimated probability of
each category for each subject is:

plum apply with pared public gpa
 /link = logit
 /print = parameter summary
 /save=estprob.

Let's apply the equations I provided previously to the data from the
FIRST subject using COMPUTE:

compute #eta0_subj1 = 2.203323 - (1.047664*0 + (-0.058683)*0 +
0.615746*3.260000).
compute #eta1_subj1 = 4.298767 - (1.047664*0 + (-0.058683)*0 +
0.615746*3.260000).

compute #cum_prob_0_subj1 = 1 / (1 + exp(-#eta0_subj1)).
compute #cum_prob_0_1_subj1 = 1 / (1 + exp(-#eta1_subj1)).
compute #cum_prob_0_1_2_subj1 = 1.

compute prob_0_subj1 = #cum_prob_0_subj1.
compute prob_1_subj1 = #cum_prob_0_1_subj1 - #cum_prob_0_subj1.
compute prob_2_subj1 = #cum_prob_0_1_2_subj1 - #cum_prob_0_1_subj1.
execute.

As you can see, the predicted probabilities for subject 1
(prob0_subj1, prob1_subj1, prob2_subj1) match exactly those produced
by the SAVE subcommand of the PLUM procedure.

Just to make sure there is no misundertanding, 2.203323 and 4.298767
are the threshold parameter estimates. 1.047664, -0.058683, and
0.615746 are the location parameter estimates. 0, 0, and 3.260000 are
the independent variable values (pared, public, and gpa, respectively)
for subject 1.

Finally, since the probability of category 0 is the highest for
subject 1 (prob_0_subj1 =.548842), it [category 0] is the predicted
category for subject 1.

Ryan

On Wed, Oct 31, 2012 at 1:15 PM, Vik Rubenfeld <[hidden email]> wrote:

>
> Very good. Thanks.
>
>
>
> --
> View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715978.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.
>
> =====================
> To manage your subscription to SPSSX-L, send a message to
> [hidden email] (not to SPSSX-L), with no body text except the
> command. To leave the list, send the command
> SIGNOFF SPSSX-L
> For a list of commands to manage subscriptions, send the command
> INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

This is fantastic. I have almost got it.

In the ucla data set, the variables pared and public have just two levels, and so they get only one parameter estimate each.  Some of the variables in my data set have 5 levels, and so get 4 parameter estimates each, one for each level minus the highest level.  Here are the parameter estimates for a test run using two predictor variables:

PLUM Q7 BY Q5_3 Q5_4
  /LINK=LOGIT
  /PRINT=PARAMETER SUMMARY
  /SAVE=ESTPROB.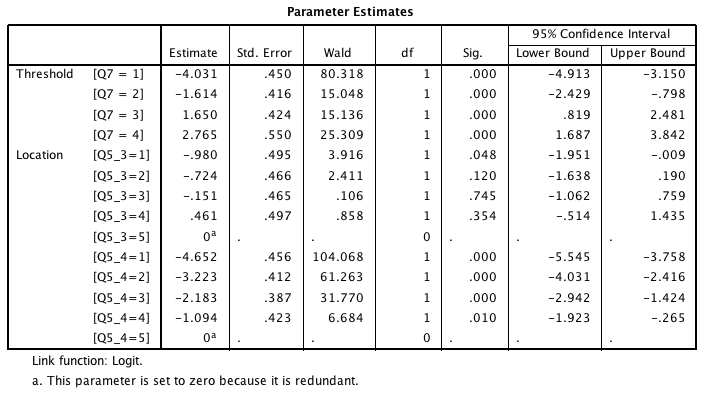



What is the correct way to apply this line of the algorithm:

   compute #eta0_subj1 = 2.203323 - (1.047664*0 + (-0.058683)*0 +
0.615746*3.260000).

...for predictor variables that have more than one parameter estimate?  In other words, which of the four possible parameter estimates is to be used?  I would have thought it would be the one that matches the observed value of the predictor variable for each case - but if the observed value is the highest possible value, then there is no matching parameter estimate. What am I missing?

I am attaching the test data set used in this example.

test-data.sav

[Ryan]

Vik,

Please do not take this the wrong way, but I'm EXTREMELY busy and
therefore cannot respond to your question in a comprehensive way.
Moreover, your question goes beyond your original question, and speaks
to a basic question about "dummy coding" (a.k.a. indicator coding) in
regression. This topic is covered in virtually any regression textbook
that I've ever seen. I'm sure it has come up a few times on SPSS-L as
well.

The concept doesn't change if you have two levels of an independent
categorical variable (e.g., gender) or multiple levels (e.g., race),
nor does it change if you're dealing with linear regression or
(binary, ordinal, etc.) logistic regression. The bottom line is that
you or the procedure if it allows for the specification of categorical
independent variables converts the single categorical independent
variable into k MINUS 1 binary (coded 0/1) "dummy variables," where k
is the number of levels of your independent categorical variable. The
k - 1 dummy variables capture all the information from the single
categorical variable. You will obtain regression coefficients
associated with each non-redundant dummy variable, and of course,
these regression coefficients along with their respective
non-redundant dummy variables need to be incorporated into the linear
predictor(s) (e.g., eta1, eta2, etc.).

Maybe somebody else is willing to jump in at this point to help you out.

Best,

Ryan

On Thu, Nov 1, 2012 at 2:40 AM, Vik Rubenfeld <[hidden email]> wrote:

> This is fantastic. I have almost got it.
>
> In the ucla data set, the variables pared and public have just two levels,
> and so they get only one parameter estimate each.  Some of the variables in
> my data set have 5 levels, and so get 4 parameter estimates each, one for
> each level minus the highest level.  Here are the parameter estimates for a
> test run using two predictor variables:
>
> PLUM Q7 BY Q5_3 Q5_4
>   /LINK=LOGIT
>   /PRINT=PARAMETER SUMMARY
>   /SAVE=ESTPROB.
>
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5715993/Screen_shot_2012-10-31_at_11.26.19_PM.png>
>
> What is the correct way to apply this line of the algorithm:
>
>    compute #eta0_subj1 = 2.203323 - (1.047664*0 + (-0.058683)*0 +
> 0.615746*3.260000).
>
> ...for predictor variables that have more than one parameter estimate?  In
> other words, which of the four possible parameter estimates is to be used?
> I would have thought it would be the one that matches the observed value of
> the predictor variable for each case - but if the observed value is the
> highest possible value, then there is no matching parameter estimate. What
> am I missing?
>
> I am attaching the test data set used in this example.
>
> test-data.sav
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5715993/test-data.sav>
>
>
>
> --
> View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715993.html
> Sent from the SPSSX Discussion mailing list archive at Nabble.com.
>
> =====================
> To manage your subscription to SPSSX-L, send a message to
> [hidden email] (not to SPSSX-L), with no body text except the
> command. To leave the list, send the command
> SIGNOFF SPSSX-L
> For a list of commands to manage subscriptions, send the command
> INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

I understand, and greatly appreciate all your help! I will look for links discussing the application of dummy variables.

Thanks again!

[Vik Rubenfeld]

From http://www.psychstat.missouristate.edu/multibook/mlt08m.html:

>>>When a researcher wishes to include a categorical variable with more than two level in a multiple regression prediction model, additional steps are needed to insure that the results are interpretable. These steps include recoding the categorical variable into a number of separate, dichotomous variables. This recoding is called "dummy coding."<<<

That looks very straightforward.

[David Marso]

A bit OT but I noticed you mentioned *way back* in the thread you were going to do this using VBA.
Before getting too committed to that approach I would suggest a gander at the VLOOKUP spreadsheet function in Excel and contemplate how it might be very handy for your implementation.  
Excel macros are great but can be a complete pain in the ass from a support perspective.  Many environments do not even allow vba code due to their 'viral' capabilities.  Also if your users have macros turned off by default you will likely receive countless support calls and emails from obnoxious higher management types ;-)
Also, after you finish would you kindly post your final solution for the benefit of others who might later have a similar query and for those who have provided assistance and might be interested in seeing it/using it?  Also be aware that some of us dinosaurs have ancient software and can't read xlsx format.

[Vik Rubenfeld]

@David, thanks for the great thoughts on Excel macros. It will be my pleasure to upload the Excel spreadsheet here.

[David Marso]

"What is the correct way to apply this line of the algorithm:

   compute #eta0_subj1 = 2.203323 - (1.047664*0 + (-0.058683)*0 +
0.615746*3.260000).

...for predictor variables that have more than one parameter estimate? "

"but if the observed value is the highest possible value, then there is no matching parameter estimate. What am I missing?":  Think about it???  If say both values are the highest category then the calculation is simply the 'threshold'.  Similarly if one or the other is zero...
---
FWIW with fair amount of confidence but not absolute certainty ;-)
These coefficients should be replaced with the full precision values .
--
COMPUTE # =
    SUM((Q5_3 EQ 1)* -.980,(Q5_3 EQ 2)*-.724,(Q5_3 EQ 3)*-.151,(Q5_3 EQ 4)*.461,
            (Q5_4 EQ 1)*-4.65,(Q5_4 EQ 2)*-3.22,(Q5_4 EQ 3)*-2.18288,(Q5_4 EQ 4) *-1.09362 ).
DO REPEAT Eta=Eta1 TO Eta4 / C=-4.03128 -1.61392 1.650025 2.764527 .
+  COMPUTE Eta=C-# .
END REPEAT.

OR

COMPUTE #=0.
DO REPEAT V=1 2 3 4  / C= -0.98 -0.724 -0.15104 0.460543.
+  IF (Q5_3  EQ V) # = #+C.
END REPEAT.
DO REPEAT V=1 2 3 4  / C=-4.65169 -3.22348 -2.18288 -1.09362 .
+  IF (Q5_4 EQ V) # = #+C.
END REPEAT.
       
DO REPEAT Eta=Eta1 TO Eta4 / C=-4.03128 -1.61392 1.650025 2.764527 .
+  COMPUTE Eta=C-# .
END REPEAT.

Don't believe me!!!! VERIFY IT and convince yourself!!!
---

Vik Rubenfeld wrote

This is fantastic. I have almost got it.

In the ucla data set, the variables pared and public have just two levels, and so they get only one parameter estimate each.  Some of the variables in my data set have 5 levels, and so get 4 parameter estimates each, one for each level minus the highest level.  Here are the parameter estimates for a test run using two predictor variables:

PLUM Q7 BY Q5_3 Q5_4
  /LINK=LOGIT
  /PRINT=PARAMETER SUMMARY
  /SAVE=ESTPROB.



What is the correct way to apply this line of the algorithm:

   compute #eta0_subj1 = 2.203323 - (1.047664*0 + (-0.058683)*0 +
0.615746*3.260000).

...for predictor variables that have more than one parameter estimate?  In other words, which of the four possible parameter estimates is to be used?  I would have thought it would be the one that matches the observed value of the predictor variable for each case - but if the observed value is the highest possible value, then there is no matching parameter estimate. What am I missing?

I am attaching the test data set used in this example.

test-data.sav

[David Marso]

Following Ryan's very enlightening discourse, my VLOOKUP idea and general WTF attitude I came up with the following incredibly fugly Excel worksheet which reproduces the SPSS calcs for the data Vik previously posted.
<see attached>

Vik Rubenfeld wrote

SpreadsheetForVLookupCatReg.xls
@David, thanks for the great thoughts on Excel macros. It will be my pleasure to upload the Excel spreadsheet here.

[David Marso]

ODD!!!! My spreadsheet ended up looking like it was part of Vik's post (quoted) It is mine and all errors or what not are all mine (same with the good stuff ;-)
--

David Marso wrote

Following Ryan's very enlightening discourse, my VLOOKUP idea and general WTF attitude I came up with the following incredibly fugly Excel worksheet which reproduces the SPSS calcs for the data Vik previously posted.
<see attached>

Vik Rubenfeld wrote

SpreadsheetForVLookupCatReg.xls
@David, thanks for the great thoughts on Excel macros. It will be my pleasure to upload the Excel spreadsheet here.

[Vik Rubenfeld]

@David, your spreadsheet perfectly matches the SPSS results of the test data! I will seek to update the format for presentation to clients and will upload results here.

@Ryan, thanks for these great algorithms!

[Vik Rubenfeld]

@David, I have implemented your formulas in a new spreadsheet, and learned a great deal in doing so.  Your algorithms improve on my understanding of how to accomplish this.  

I am continuing to work on formatting and will upload the completed spreadsheet when it is ready.

[David Marso]

I learned alot from doing it too.  For one thing I hadn't realized my 11.5 (2003) had PLUM ;-)
Also developed a new appreciation of VLOOKUP (very powerful device/technique for this).
VLOOKUP drives a lot of the internals.  When you do your formatting consider moving the calcs and parameters to separate sheets and protecting them.  Also impose validation in the input fields and add a means for supporting covariates.  Note that most if not all of the formula can be extended by dragging ;-)
---

Vik Rubenfeld wrote

@David, I have implemented your formulas in a new spreadsheet, and learned a great deal in doing so.  Your algorithms improve on my understanding of how to accomplish this.  

I am continuing to work on formatting and will upload the completed spreadsheet when it is ready.

[Vik Rubenfeld]

Attached please find the revised spreadsheet. As requested, it is in .xls format, and uses no macros.

Thank you so much to David, Ryan, and all on this thread for your help!

Classifying_New_Cases_via_Ord_Regression.xls