How to do a Ladder graph
|
In do not have access to my notes and files and the moment.
I have often found that it helps clients to understand a pre-post difference to construct a ladder graph. This graph has 2 vertical axes with the same scaling. e.g., percentiles, z-scores, or in the example below the mean of a summative score with items on 1 to 7 response scale. There is a rung for each case. The rung connects the value for the pretest to the value for the posttest for that case. data list list/PreTest PostTest (2f3.1). begin data 4.1 4.3 2.5 5.3 4.6 3.3 4.1 4.8 3.3 5.6 3.6 3.8 3.0 5.7 4.1 1.7 4.5 4.8 5.2 3.5 4.6 4.3 3.6 4.5 3.6 5.0 4.1 4.8 4.3 4.1 5.3 2.5 3.3 4.6 4.8 4.1 5.6 3.3 3.8 3.6 5.7 3.0 1.7 4.1 4.8 4.5 3.5 5.2 4.3 4.6 4.5 3.6 5.0 3.6 4.8 4.1 5.3 5.3 5.5 5.5 6.1 6.1 end data. descriptives variables = PreTest PostTest. This works well when there is only a small n.
Art Kendall
Social Research Consultants |
|
I'm not familiar with ladder graphs but it sounds to me that you want something like the plot that is produced in GLM whencompute group=$casenum. GLM PreTest PostTest by group/ wsfactor=pre_post(2)/ WSDESIGN=pre_post/ PLOT=PROFILE (pre_post*group). I'd be interesting in learning to create a "correct" version On Sat, Jan 30, 2016 at 12:02 PM, Art Kendall <[hidden email]> wrote: In do not have access to my notes and files and the moment. |
|
In reply to this post by Art Kendall
Is this what you mean Art?
GGRAPH /GRAPHDATASET NAME="graphdataset" VARIABLES=PreTest PostTest MISSING=LISTWISE REPORTMISSING=NO /GRAPHSPEC SOURCE=INLINE. BEGIN GPL SOURCE: s=userSource(id("graphdataset")) DATA: PreTest=col(source(s), name("PreTest")) DATA: PostTest=col(source(s), name("PostTest")) TRANS: pre = eval("Pre") TRANS: pos = eval("Post") GUIDE: axis(dim(1)) GUIDE: axis(dim(2), label("Test Scores")) ELEMENT: edge(position((pre*PreTest)+(pos*PostTest))) END GPL. 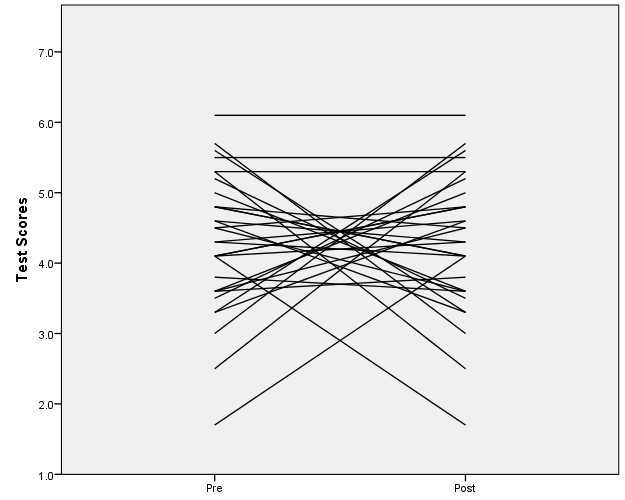 I wrote an article about why I don't like these types of slopegraphs, http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2410875, a scatterplot is almost always better. For example here with the scatterplot the scores have an obvious negative correlation, and the three scores that have equal pre-post are outliers. GGRAPH /GRAPHDATASET NAME="graphdataset" VARIABLES=PreTest PostTest MISSING=LISTWISE REPORTMISSING=NO /GRAPHSPEC SOURCE=INLINE. BEGIN GPL SOURCE: s=userSource(id("graphdataset")) DATA: PreTest=col(source(s), name("PreTest")) DATA: PostTest=col(source(s), name("PostTest")) GUIDE: axis(dim(1), label("PreTest")) GUIDE: axis(dim(2), label("PostTest")) ELEMENT: line(position(PreTest*PreTest)) ELEMENT: point(position(PreTest*PostTest)) END GPL. 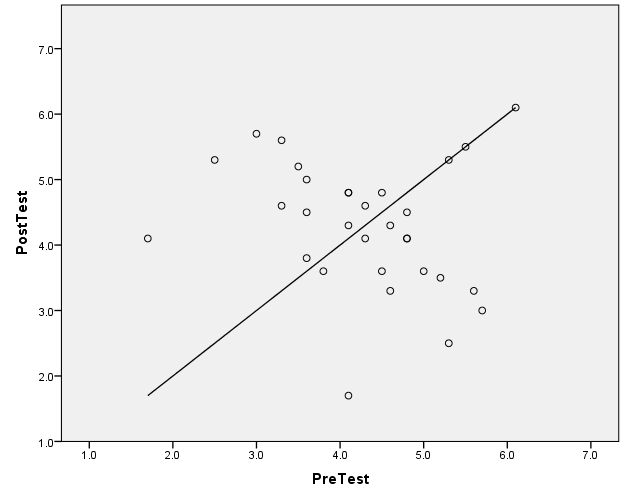
|
|
Thanks to both list members who responded.
I concur that ladder graphs are sub-optimal when only one visualization is used (e.g., in a publication). Both what you suggested and what Michael Palij suggested produce visualizations to emphasize the there are differences among individuals. However, in a repeated measure situation such as a pre-test with post test after a treatment/lesson/etc, or test-retest reliability it has been my experience it helps clients/students understand to use 3 visualizations. A scatter plot, a ladder graph, and box plots. Sometimes it helps understanding to randomize the post-test a few times and show how the different plots change. ---- One of my soapboxes is that it is fruitful to look at data in multiple ways. --- P.S. wrt parallel coordinate plots, the older type of profile plot which is a specific type of parallel coordinate plot has been very useful in interpreting profiles derived via clustering. The profile plot Michael Palij produces a ladder graph which is useful as an additional perspective. However, in other situations (e.g., cluster profiles) the profile plot without the repeated vertical axes can be affected by seeming vertical drift since in clustering the information is the shape (also elevation, and scatter) of the profile rather than trend as in time series.
Art Kendall
Social Research Consultants |
|
Administrator
|
I agree with Art's soapbox point below.
When teaching one-way repeated measures ANOVA, I use a plot similar to the ladder graph Andy generated above (but with 3 conditions/treatments, not 2) to talk about the Treatment x Subject interaction term, which is the error term for that model. As for any other interaction, the more the lines depart from parallel, the greater the interaction effect--and in that particular context, the larger the MS_error, so the smaller the F-ratio (all other things being equal).
--
Bruce Weaver bweaver@lakeheadu.ca http://sites.google.com/a/lakeheadu.ca/bweaver/ "When all else fails, RTFM." PLEASE NOTE THE FOLLOWING: 1. My Hotmail account is not monitored regularly. To send me an e-mail, please use the address shown above. 2. The SPSSX Discussion forum on Nabble is no longer linked to the SPSSX-L listserv administered by UGA (https://listserv.uga.edu/). |
|
Just to add to Bruce's comment below, specifically "all other
things being equal", let's consider the classic Reaction Time (RT) experiment by Donders which uses a one-way three level within-subject design where the levels refer to different RT tasks: (1) Simple RT: press a button/key on a keyboard as soon as a colored visual stimulus (e.g., a square) or auditory stimulus is presented (2) Go-No Go RT: press a button to one specific color/sound but do not respond to any other color/sound (3) Choice RT: press one button if one specific color/sound is presented, press another button if another color/sound is presented (both version of this experiment is available on the http://opl.apa.org website; look under the studies tab on the homepage). In general, we refer to the analysis of such a design as using a one-way repeated measures ANOVA but some sources refer to the analysis as "two-way ANOVA without replication". Glass and Hopkins in their stat text point this out (in the different editions) but perhaps more importantly, if one wanted to do a one-way repeated measure ANOVA in Excel (after activating the toolpak), the analysis that one would select from the list of ANOVA analyses is "two-way ANOVA without replication". At first glance, this might be strange until one understand the logic of the repeated measures ANOVA. The analysis assumes that there are two sources that produce systematic variance in the dependent variable (in the Donders' case, it would be variance in RT performance): (A) Differences among Subjects: since subjects/participants have multiple measurement made on them, we can calculate a mean for each subject and we expect that subjects will systematically differ from each other. This results in a reduction in what would have been part if the error term -- in old version of SAS one had to specify what error terms to use in GLM and some folks treated within-subject designs as between-subjects design, leaving out the subject effect which was added to a single error term (one dissertation I was a reader on did this and the analyses had to be redone). SAS implemented the "repeated" keyword/command which I think should have helped stopped this problem from occurring (SPSS and BMDP inferred the structure of the design from how the data was specified). NOTE: If subjects DO NOT DIFFER, then an independent groups ANOVA should be done because the subject variance will still be subtracted from the error term (subject by treatment interaction), an unwarranted reduction in the error term. (B) Differences among levels of the independent variable: in the Donders example, this represents differences among the mean RT for each task. In Excel, the "two-way ANOVA without replication" provides the following output: (a) Subject means/desc stats: the mean/variance across the levels of independent variable for each subject (b) Treatment means/desc stats: the mean/variance for each level of the independent variable (in the Donders task, the mean RT for each task). The (classic) simplified ANOVA table produced in Excel has three sources of variance: (i) Rows: differences among subjects; this should be statistically significant but most people just ignore this entry (ii) Columns: difference among treatment levels (in the Donders task, the means for the Simple, Go-No Go, and Choice RT task) (iii) Error Term: the subject by treatment interaction (this is what Bruce refers to below). The key point that I want to make is the differences among subjects, as reflected in the Row entry above or the Between-Subjects table in SPSS, has a greater effect on the error term than the degree of interaction. The larger the difference among subjects/participants, the smaller the error term, no matter how big the interaction is. An additional point is the degree of correlation between values at different levels of the independent variable -- higher correlations will produce stronger subject effects. To better under this point, consider the correlated groups t-test; one form of the formula is: t = (M1 - M2) /sqrt(VarErr1 + VarErr2 - 2*r*SE1*SE2) The denominator/error term consists of: Variance errors for each group (i.e., VarErr1, VarErr2) Standard errors for each group (I.e., SE1, SE2) Pearson r between pairs of values (i.e., r) and the constant 2. The larger the correlation is between value for the two levels of the independent variable, the smaller the error term. If the Pearson r = 0, the test become the independent groups t-test. A similar logic holds for ANOVA: the higher the correlation between values for different levels of the independent variable, the smaller the error term, regardless of the size of the interaction. Reaction Time studies typically show big subject effects, especially if there is a large range of ages (e.g., 18 -50). With other dependent measures, YMMV. HTH. -Mike Palij New York University [hidden email] ----- Original Message ----- On Sunday, January 31, 2016 4:41 PM, Bruce Weaver wrote: > >I agree with Art's soapbox point below. > > When teaching one-way repeated measures ANOVA, I use a plot similar to > the > ladder graph Andy generated above (but with 3 conditions/treatments, > not 2) > to talk about the Treatment x Subject interaction term, which is the > error > term for that model. As for any other interaction, the more the lines > depart from parallel, the greater the interaction effect--and in that > particular context, the larger the MS_error, so the smaller the > F-ratio (all > other things being equal). > > > > Art Kendall wrote >> Thanks to both list members who responded. >> I concur that ladder graphs are sub-optimal when only one >> visualization is >> used (e.g., in a publication). >> >> Both what you suggested and what Michael Palij suggested produce >> visualizations to emphasize the there are differences among >> individuals. >> >> However, in a repeated measure situation such as a pre-test with >> post >> test after a treatment/lesson/etc, or test-retest reliability it has >> been >> my experience it helps clients/students understand to use 3 >> visualizations. A scatter plot, a ladder graph, and box plots. >> >> Sometimes it helps understanding to randomize the post-test a few >> times >> and show how the different plots change. >> ---- >> One of my soapboxes is that it is fruitful to look at data in >> multiple >> ways. >> --- >> P.S. wrt parallel coordinate plots, the older type of profile plot >> which >> is a specific type of parallel coordinate plot has been very useful >> in >> interpreting profiles derived via clustering. >> >> The profile plot Michael Palij produces a ladder graph which is >> useful as >> an additional perspective. >> However, in other situations (e.g., cluster profiles) the profile >> plot >> without the repeated vertical axes can be affected by seeming >> vertical >> drift since in clustering the information is the shape (also >> elevation, >> and scatter) of the profile rather than trend as in time series. > > > > > > ----- > -- > Bruce Weaver > [hidden email] > http://sites.google.com/a/lakeheadu.ca/bweaver/ > > "When all else fails, RTFM." > > NOTE: My Hotmail account is not monitored regularly. > To send me an e-mail, please use the address shown above. > > -- > View this message in context: > http://spssx-discussion.1045642.n5.nabble.com/How-to-do-a-Ladder-graph-tp5731410p5731414.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except > the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
Mostly, good and useful comments, but ...
=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD
> Date: Mon, 1 Feb 2016 13:21:54 -0500 > From: [hidden email] > Subject: Re: How to do a Ladder graph > To: [hidden email] > ... > > (A) Differences among Subjects: since subjects/participants have > multiple measurement made on them, we can calculate a mean > for each subject and we expect that subjects will systematically > differ from each other. This results in a reduction in what would > have been part if the error term -- in old version of SAS one had > to specify what error terms to use in GLM and some folks treated > within-subject designs as between-subjects design, leaving out > the subject effect which was added to a single error term (one > dissertation I was a reader on did this and the analyses had to > be redone). SAS implemented the "repeated" keyword/command > which I think should have helped stopped this problem from > occurring (SPSS and BMDP inferred the structure of the design > from how the data was specified). > NOTE: If subjects DO NOT DIFFER, then an independent > groups ANOVA should be done because the subject variance > will still be subtracted from the error term (subject by treatment > interaction), an unwarranted reduction in the error term. My reaction to the Note: NO! - "DO NOT DIFFER" is apparently a description of a test result, since the next phrases describe subtracting variances... Someone is claiming that what must be described as analyzing "according to the actual design" would provide "an unwarranted reduction in the error term"? I admit that the common examples won't show much difference. But I recall an extreme example: Consider a paired t-test with very similar means and a highly negative correlation. (Fish were faced with a forced choice, target A vs target B, and the time spent for A+B was always 10 or close to it.) - The test with-versus-without the subject effect changes both the sum of squares (minimally, in this example) and the d.f. (a lot, in this example). Ignoring pairing in the paired t-test, which is the simplest Repeated Measure, gives a test that is too weak when the correlation is positive and too strong when it is negative (ignoring cases where tiny d.f. affects the power). I can't agree that it is ever a mistake to analyze according to the design; though the observation that a variance is exactly ZERO raises the question of "What does describe this design?" -- Rich Ulrich |
|
Administrator
|
Thanks Rich. I had a similar reaction to that NOTE, but didn't have time today to articulate it.
--
Bruce Weaver bweaver@lakeheadu.ca http://sites.google.com/a/lakeheadu.ca/bweaver/ "When all else fails, RTFM." PLEASE NOTE THE FOLLOWING: 1. My Hotmail account is not monitored regularly. To send me an e-mail, please use the address shown above. 2. The SPSSX Discussion forum on Nabble is no longer linked to the SPSSX-L listserv administered by UGA (https://listserv.uga.edu/). |
|
In reply to this post by Rich Ulrich
----- Original Message -----
On Monday, February 01, 2016 8:44 PM,Rich Ulrich wortel > >Mostly, good and useful comments, but ... Thank you. However, some of the comments you make below are unclear to me and perhaps you can clarify them a little On Mon, 1 Feb 2016 13:21:54 -0500, Mike Palij wrote: >> (A) Differences among Subjects: since subjects/participants have >> multiple measurement made on them, we can calculate a mean >> for each subject and we expect that subjects will systematically >> differ from each other. If one has access to Glass & Hopkins, 1st edition, see Table 19.6, p463 or If one has access to Glass & Hopkins, 3rd edition, see Table 20.1, p575 (the latter resembles the output from Excel more than the former). I will use their terms and indexes in the equations I present below: In the decomposition of the Sum of Squares in the repeated measures ANOVA, the equation for the Total sum of square (SS-total) is divided into the following components:: SS-total = SS-Treatment(T) + SS-Subjects(P) + SS-Error(TxP) NOTE: Glass & Hiopkins use T to refer to the Treatement variable and t for the level of T; sum of t = T, the total number of treatments. P is used to refer to the total number of Persons or Subjects and p is used to refer to a specific person/subject; sum(p) = P, or the number of subjects. This makes the presentation consistent with that of Glass & Hopkins, 1st edition, Table 19.6, p 463 and Glass & Hopkins, 3rd Ed, Table 20.1, p 574 SS-Subjects = sum(Mean for Subject p - Grand Mean)^2 To simply notion, let (Mean for Subject p -Grand Mean) = alpha-p and let (mean for Subject p - Grand mean) ^2 = alpha-p^2 which provides SS-Subjects = sum(alpha-p^2 df-subjects or DF-P = P -1 or the number subjects/persons - 1 MS-Subjects = SS-Subject / df-subjests SS-Treatment = sum(Mean for Treatment level t - Grand Mean^2 To simplify notation, llet (Mean for Treatment level t - Grand Mean) = beta-t and (mean for Treatment level t - Grand Mean)^2 = beta-t^2 SS-Treatments= sum(beta-t^2) df-Treatment or DF-T = T -1 or the number of treatment levels -1 The calculation of SS-Error(TxP) or the interaction between subjects and treaments is laborious by hand so simple formula to obtain it (under the assumption all the math done so far is correct) is: SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment NOTE: It is assumed that both SS-Subject and SS-Treatment represent systematic sources of variance, so substracting them from SS-total should provide a sum of squares that reflects random error. But if SS-Subjects(P) is NOT A SOURCE OF SIGNIFICANT VARIANCE THEN SUBTRACTING IT FROM SS-Total will cause SS-Error to be underestimated. So, it should be obvious that if there are no significant differences among subjects in a within-subject design, it is inappropriate to calcualte the SS-Subjects/Persons and substract it from SS-Total to get the the SS-error -- one should do an independnet groups ANOVA instead. Things might be clearer in the correlated group t-test. Recall the formula for it is: t = (M1 - M2) /sqrt(VarErr1 + VarErr2 - 2*r*SE1*SE2) Now, according to Hoyle, if the Pearson f is not significant then the entire term -2*r*SE1*SE2 should be set to zero and one is left with a version of the independent groups t-test. But if one leaves that term while r is not significant, it will reduce the error variance (i.e, sum of VarErr1 + VarErr2)) and make the donominator inappropriately smaller. How much of an effect this has on the t-test depends upon how large the nonsignificant - 2*r*SE1*SE2 is but it could provide seriously misleading results. Why not simply do the correct test for the situation one has? Is some statistical religious law being violated if one does so? >>This results in a reduction in what would >> have been part if the error term -- in old version of SAS one had >> to specify what error terms to use in GLM and some folks treated >> within-subject designs as between-subjects design, leaving out >> the subject effect which was added to a single error term (one >> dissertation I was a reader on did this and the analyses had to >> be redone). SAS implemented the "repeated" keyword/command >> which I think should have helped stopped this problem from >> occurring (SPSS and BMDP inferred the structure of the design >> from how the data was specified). >> NOTE: If subjects DO NOT DIFFER, then an independent >> groups ANOVA should be done because the subject variance >> will still be subtracted from the error term (subject by treatment >> interaction), an unwarranted reduction in the error term. > >My reaction to the Note: NO! - "DO NOT DIFFER" is apparently a >description of >a test result, since the next phrases describe subtracting variances... Yes, see above: SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment >Someone is claiming that what must be described as analyzing "according >to >the actual design" would provide "an unwarranted reduction in the >error term"? If one asserts that one is using a within-subject design but (when T > 2) and the variance-covariance matrix is an idtentity matrix (that is, the responses are not correlated as one would expect and which a repeated-measures ANOVA assumes), then one really shouldn't do a repeated measure ANOVA because SS-Subjects will be calcualted and as a sample value is unlikely to be exactly equal to zero, thus giving rise to an inappropriate SS-Error(TxP) if one is using the formula (the alternative is to take the cell mean for the combination Tt by Pp and subtract the Treatment mean for that t level + subtract the Subject mean for the p level +the grand mean -- a hand operation that probably drove many students mad, using the following is so much easier if one has been doing the math correctly: SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment >I admit that the common examples won't show much difference. But I >recall >an extreme example: Consider a paired t-test with very similar means >and >a highly negative correlation. We've done this dance before and simply put I doubt that Gosset/Student or Sir Ronald ever considered the case where measuring the same individual twice would lead to a negative correlation because this occurs only in rare situations. If the negative correlation is "real", then I think one has a couple of options: (1) take the absolute value off the negative pearson r, do the appropriate calculation, and see if it make sense, or (2) Make up you own damned test. If you have a pair of values x and y on the same individual, then Y would have to be blow the Y mean in order to obtain a negative correlation. Given that Gosset's concerns was with making sure that contents of vats of ale and stout did not vary significantly from vat to vat, I think that Guinness would have fired his ass if he ever obtain a negative correlation between two measures that should be the same. If you are studying fish that give rise to strange patterns that are not appropriate for existing tests, then this is a wonderful opportunity for one to come up with a new test -- afterall they might name after you, especially if some else created the test before; see: https://en.wikipedia.org/wiki/Stigler's_law_of_eponymy [snip] >I can't agree that it is ever a mistake to analyze according to the >design; >though the observation that a variance is exactly ZERO raises the >question >of "What does describe this design?" I think you are unclear here. If you do a two-level within-subject design and obtain a nonsignificant Pearson of 0.10, between your two measures, are you saying that you should still use a correlated groups t-test -- even if you ave no evidence of a correlation between your pairs? Indeed you have evidence that the sample Pearson r should be set to zero, then the term - 2*r*SE1*SE2 in the denominator should be set to zero. If you do not set it to zero because you think that even without evidence of r > 0.00 you are "entitled" to do that version of the test, I'd really like to hear the justification and why it makes any sense instead of a misleading result. -Mike Palij New York University [hidden email] ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
Administrator
|
I don't have time to get fully engaged in this discussion right now, but I do have the 3rd Edition of Glass & Hopkins, so decided to run their one-way repeated measures ANOVA example. Here's the syntax:
* One-way repeated measures ANOVA from Table 20.1 * in 3rd Edition of Glass & Hopkins (p. 574). DATA LIST list / ID T1 to T5 (6F2.0). BEGIN DATA 1 1 2 4 5 6 2 1 1 3 5 6 3 1 2 5 7 6 4 2 1 4 6 7 5 3 3 5 8 8 6 2 2 4 7 8 7 1 3 4 6 7 8 0 2 5 7 8 9 3 3 6 8 9 10 2 2 4 7 8 END DATA. GLM T1 T2 T3 T4 T5 /WSFACTOR=Treatment 5 Polynomial /METHOD=SSTYPE(3) /PLOT=PROFILE(Treatment) /EMMEANS=TABLES(Treatment) /CRITERIA=ALPHA(.05) /WSDESIGN=Treatment. * Results match those shown by G&H. * SS_subjects = SS_error in the "Tests of Between * Subjects Effects" table. * SS_T and SS_T*S are in the sphericity assumed * rows in the "Tests of Within Subjects Effects" table. * Results for polynomial contrasts also match G&H results. CORRELATIONS T1 to T5. Here are the SS from that model (using sphericity assumed results): SS_Between-Ss = 26.8 SS_Within-Ss = 277.2 SS_T = 263.8 SS_TxS = 13.4 SS_Total = 304 These results match those shown by G&H in their Table 20.1. And here is the correlation matrix (view in fixed font): Correlations T1 T2 T3 T4 T5 T1 Pearson Correlation 1 .374 .355 .578 .565 Sig. (2-tailed) .287 .315 .080 .089 N 10 10 10 10 10 T2 Pearson Correlation .374 1 .643 .616 .526 Sig. (2-tailed) .287 .045 .058 .118 N 10 10 10 10 10 T3 Pearson Correlation .355 .643 1 .809 .597 Sig. (2-tailed) .315 .045 .005 .068 N 10 10 10 10 10 T4 Pearson Correlation .578 .616 .809 1 .800 Sig. (2-tailed) .080 .058 .005 .005 N 10 10 10 10 10 T5 Pearson Correlation .565 .526 .597 .800 1 Sig. (2-tailed) .089 .118 .068 .005 N 10 10 10 10 10 I know I said I didn't have time to get engaged too deeply in this, but now I'm curious. In this example, SS_Between-Ss is pretty small relative to SS_Total (8.8% of the total SS, approximately). And only 3 of the 10 correlations achieve statistical significance at the .05 level (r_23, r_34 and r_45). From your point of view, Mike, how would this affect the way you analyze the data? Or would it? Cheers, Bruce
--
Bruce Weaver bweaver@lakeheadu.ca http://sites.google.com/a/lakeheadu.ca/bweaver/ "When all else fails, RTFM." PLEASE NOTE THE FOLLOWING: 1. My Hotmail account is not monitored regularly. To send me an e-mail, please use the address shown above. 2. The SPSSX Discussion forum on Nabble is no longer linked to the SPSSX-L listserv administered by UGA (https://listserv.uga.edu/). |
|
Okay, I'll try to keep this brief:
(1) Don't use N=10 in real life if you're doing research unless you are sure that the effects are huge, otherwise, your tests will be severely underpowered. An obtained correlation would have to be greater than r(8) = 0.632 in order to be significant at the .05 level (two-tailed). Cohen (1992; Power Primer in Psych Bull) has r= .50 as a "large" effect, so any correlation would have to be extra large to be significant. If you run the variables t1 to t5 through the reliability procedure, you'll see that he mean correlation r=0.586 or greater than large by Cohen's criteria, the minimum r=.355 which would require about N=45 to be significant at alpha= .05, two-tailed. NOTE: r(8) = 0.632 and other values are obtained from Table 8.6 for critical r for different df in Gravetter & Wallnau's text; but I'm sure there's a similar one in Glass & Hopkins Morale: If you're constructing a dataset for pedagogical purposes, then keeping sample size small for a constructed dataset makes for good example or homework but bad research. (2) I'm not sure what your point is with the correlation matrix given what I say in (1) above but I think that maybe what you really wanted to do is test the hypothesis that the correlation matrix is equal to an identity matrix, that is, none of the correlations is significant. However, for N=10, lack of power would probably make the test inconclusive. (3) As important as the correlations are in this situation the question of whether there are significant differences among subjects is more important because of how the error term is calculated. Recall: SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment(T) Unfortunately, the SPSS output does not provide the F for differences among subjects so one does not really know if there are significant differences among subjects (one could do hand calculations). Excel does provide this value and it is F(9,49) = 8.00, p< .001 which means that calculating the SS-error using the formula above is appropriate. It should be obvious that if this F was not significant, one would have an inappropriate error term (as long as lack of power were not the reason). One really should do this check. (2) Finally, the Mauchly test for sphericity is nonsignificant, so you can assume that you have sphericity though this is probably underpowered as well. Note that we don't need "compound symmetry" (equal variances and equal correlations) instead a pattern of different variances and/or correlations could meet the criteria for sphericity. But let me point out that if one views this as a 2-way ANOVA without replication, it should be obvious that we have a mixed design: the trials/treatment are a fixed effect and subjects are a random effect. I believe one could use the Mixed procedure in SPSS and try out various variance-covariance matrices to do a more appropriate analysis but I'll leave to other who are familiar with the procedure. I hope that I've answered you questions. -Mike Palij New York University [hidden email] ----- Original Message ----- From: "Bruce Weaver" <[hidden email]> To: <[hidden email]> Sent: Tuesday, February 02, 2016 6:27 PM Subject: Re: How to do a Ladder graph >I don't have time to get fully engaged in this discussion right now, >but I do > have the 3rd Edition of Glass & Hopkins, so decided to run their > one-way > repeated measures ANOVA example. Here's the syntax: > > * One-way repeated measures ANOVA from Table 20.1 > * in 3rd Edition of Glass & Hopkins (p. 574). > > DATA LIST list / ID T1 to T5 (6F2.0). > BEGIN DATA > 1 1 2 4 5 6 > 2 1 1 3 5 6 > 3 1 2 5 7 6 > 4 2 1 4 6 7 > 5 3 3 5 8 8 > 6 2 2 4 7 8 > 7 1 3 4 6 7 > 8 0 2 5 7 8 > 9 3 3 6 8 9 > 10 2 2 4 7 8 > END DATA. > > GLM T1 T2 T3 T4 T5 > /WSFACTOR=Treatment 5 Polynomial > /METHOD=SSTYPE(3) > /PLOT=PROFILE(Treatment) > /EMMEANS=TABLES(Treatment) > /CRITERIA=ALPHA(.05) > /WSDESIGN=Treatment. > > * Results match those shown by G&H. > * SS_subjects = SS_error in the "Tests of Between > * Subjects Effects" table. > * SS_T and SS_T*S are in the sphericity assumed > * rows in the "Tests of Within Subjects Effects" table. > * Results for polynomial contrasts also match G&H results. > > CORRELATIONS T1 to T5. > > > Here are the SS from that model (using sphericity assumed results): > > SS_Between-Ss = 26.8 > SS_Within-Ss = 277.2 > SS_T = 263.8 > SS_TxS = 13.4 > SS_Total = 304 > > These results match those shown by G&H in their Table 20.1. > > And here is the correlation matrix (view in fixed font): > > Correlations > T1 T2 T3 T4 T5 > T1 Pearson Correlation 1 .374 .355 .578 .565 > Sig. (2-tailed) .287 .315 .080 .089 > N 10 10 10 10 10 > T2 Pearson Correlation .374 1 .643 .616 .526 > Sig. (2-tailed) .287 .045 .058 .118 > N 10 10 10 10 10 > T3 Pearson Correlation .355 .643 1 .809 .597 > Sig. (2-tailed) .315 .045 .005 .068 > N 10 10 10 10 10 > T4 Pearson Correlation .578 .616 .809 1 .800 > Sig. (2-tailed) .080 .058 .005 .005 > N 10 10 10 10 10 > T5 Pearson Correlation .565 .526 .597 .800 1 > Sig. (2-tailed) .089 .118 .068 .005 > N 10 10 10 10 10 > > > I know I said I didn't have time to get engaged too deeply in this, > but now > I'm curious. In this example, SS_Between-Ss is pretty small relative > to > SS_Total (8.8% of the total SS, approximately). > > And only 3 of the 10 correlations achieve statistical significance at > the > .05 level (r_23, r_34 and r_45). > > From your point of view, Mike, how would this affect the way you > analyze the > data? Or would it? > > Cheers, > Bruce > > > > Mike wrote >> ----- Original Message ----- >> On Monday, February 01, 2016 8:44 PM,Rich Ulrich wortel >>> >>>Mostly, good and useful comments, but ... >> >> Thank you. However, some of the comments you make below >> are unclear to me and perhaps you can clarify them a little >> >> On Mon, 1 Feb 2016 13:21:54 -0500, Mike Palij wrote: >>>> (A) Differences among Subjects: since subjects/participants have >>>> multiple measurement made on them, we can calculate a mean >>>> for each subject and we expect that subjects will systematically >>>> differ from each other. >> >> If one has access to Glass & Hopkins, 1st edition, see Table 19.6, >> p463 >> or >> If one has access to Glass & Hopkins, 3rd edition, see Table 20.1, >> p575 >> (the latter resembles the output from Excel more than the former). >> I will use their terms and indexes in the equations I present below: >> >> In the decomposition of the Sum of Squares in the repeated measures >> ANOVA, the equation for the Total sum of square (SS-total) is >> divided into the following components:: >> >> SS-total = SS-Treatment(T) + SS-Subjects(P) + SS-Error(TxP) >> >> NOTE: Glass & Hiopkins use T to refer to the Treatement variable >> and t for the level of T; sum of t = T, the total number of >> treatments. >> >> P is used to refer to the total number of Persons or Subjects and >> p is used to refer to a specific person/subject; sum(p) = P, or >> the number of subjects. >> >> This makes the presentation consistent with that >> of Glass & Hopkins, 1st edition, Table 19.6, p 463 and >> Glass & Hopkins, 3rd Ed, Table 20.1, p 574 >> >> SS-Subjects = sum(Mean for Subject p - Grand Mean)^2 >> To simply notion, let (Mean for Subject p -Grand Mean) = alpha-p >> and let (mean for Subject p - Grand mean) ^2 = alpha-p^2 >> which provides >> SS-Subjects = sum(alpha-p^2 >> >> df-subjects or DF-P = P -1 or the number subjects/persons - 1 >> >> MS-Subjects = SS-Subject / df-subjests >> >> SS-Treatment = sum(Mean for Treatment level t - Grand Mean^2 >> To simplify notation, llet (Mean for Treatment level t - Grand Mean) >> = >> beta-t >> and (mean for Treatment level t - Grand Mean)^2 = beta-t^2 >> SS-Treatments= sum(beta-t^2) >> >> df-Treatment or DF-T = T -1 or the number of treatment levels -1 >> >> The calculation of SS-Error(TxP) or the interaction between subjects >> and >> treaments is laborious by hand so simple formula to obtain it (under >> the >> assumption all the math done so far is correct) is: >> >> SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment >> >> NOTE: It is assumed that both SS-Subject and SS-Treatment represent >> systematic sources of variance, so substracting them from SS-total >> should provide a sum of squares that reflects random error. But if >> SS-Subjects(P) is NOT A SOURCE OF SIGNIFICANT VARIANCE >> THEN SUBTRACTING IT FROM SS-Total will cause SS-Error to be >> underestimated. >> >> So, it should be obvious that if there are no significant differences >> among subjects in a within-subject design, it is inappropriate to >> calcualte >> the SS-Subjects/Persons and substract it from SS-Total to get the >> the SS-error -- one should do an independnet groups ANOVA instead. >> >> Things might be clearer in the correlated group t-test. Recall the >> formula for it is: >> >> t = (M1 - M2) /sqrt(VarErr1 + VarErr2 - 2*r*SE1*SE2) >> >> Now, according to Hoyle, if the Pearson f is not significant >> then the entire term -2*r*SE1*SE2 should be set to zero and >> one is left with a version of the independent groups t-test. >> But if one leaves that term while r is not significant, it will >> reduce >> the >> error variance (i.e, sum of VarErr1 + VarErr2)) and make the >> donominator inappropriately smaller. How much of an effect >> this has on the t-test depends upon how large the nonsignificant >> - 2*r*SE1*SE2 is but it could provide seriously misleading >> results. >> >> Why not simply do the correct test for the situation one has? >> Is some statistical religious law being violated if one does so? >> >>>>This results in a reduction in what would >>>> have been part if the error term -- in old version of SAS one had >>>> to specify what error terms to use in GLM and some folks treated >>>> within-subject designs as between-subjects design, leaving out >>>> the subject effect which was added to a single error term (one >>>> dissertation I was a reader on did this and the analyses had to >>>> be redone). SAS implemented the "repeated" keyword/command >>>> which I think should have helped stopped this problem from >>>> occurring (SPSS and BMDP inferred the structure of the design >>>> from how the data was specified). >>>> NOTE: If subjects DO NOT DIFFER, then an independent >>>> groups ANOVA should be done because the subject variance >>>> will still be subtracted from the error term (subject by treatment >>>> interaction), an unwarranted reduction in the error term. >>> >>>My reaction to the Note: NO! - "DO NOT DIFFER" is apparently a >>>description of >>>a test result, since the next phrases describe subtracting >>>variances... >> >> Yes, see above: >> >> SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment >> >>>Someone is claiming that what must be described as analyzing >>>"according >>>to >>>the actual design" would provide "an unwarranted reduction in the >>>error term"? >> >> If one asserts that one is using a within-subject design but (when T >> > >> 2) and the >> variance-covariance matrix is an idtentity matrix (that is, the >> responses are >> not correlated as one would expect and which a repeated-measures >> ANOVA >> assumes), then one really shouldn't do a repeated measure ANOVA >> because >> SS-Subjects will be calcualted and as a sample value is unlikely to >> be >> exactly >> equal to zero, thus giving rise to an inappropriate SS-Error(TxP) if >> one >> is >> using the formula (the alternative is to take the cell mean for the >> combination Tt by Pp >> and subtract the Treatment mean for that t level + subtract the >> Subject >> mean for the >> p level +the grand mean -- a hand operation that probably drove many >> students >> mad, using the following is so much easier if one has been doing the >> math correctly: >> >> SS-Error(TxP) = SS-total - SS-Subjects(P) - SS-Treatment >> >>>I admit that the common examples won't show much difference. But I >>>recall >>>an extreme example: Consider a paired t-test with very similar means >>>and >>>a highly negative correlation. >> >> We've done this dance before and simply put I doubt that >> Gosset/Student >> or >> Sir Ronald ever considered the case where measuring the same >> individual >> twice would lead to a negative correlation because this occurs only >> in >> rare situations. If the negative correlation is "real", then I think >> one has a couple >> of options: >> (1) take the absolute value off the negative pearson r, do the >> appropriate calculation, >> and see if it make sense, >> or >> (2) Make up you own damned test. If you have a pair of values x and >> y >> on the same >> individual, then Y would have to be blow the Y mean in order to >> obtain a >> negative >> correlation. Given that Gosset's concerns was with making sure that >> contents of >> vats of ale and stout did not vary significantly from vat to vat, I >> think that Guinness >> would have fired his ass if he ever obtain a negative correlation >> between two measures >> that should be the same. >> >> If you are studying fish that give rise to strange patterns that are >> not >> appropriate >> for existing tests, then this is a wonderful opportunity for one to >> come >> up with >> a new test -- afterall they might name after you, especially if some >> else created >> the test before; see: >> https://en.wikipedia.org/wiki/Stigler's_law_of_eponymy >> >> [snip] >>>I can't agree that it is ever a mistake to analyze according to the >>>design; >>>though the observation that a variance is exactly ZERO raises the >>>question >>>of "What does describe this design?" >> >> I think you are unclear here. If you do a two-level within-subject >> design >> and obtain a nonsignificant Pearson of 0.10, between your two >> measures, >> are you saying that you should still use a correlated groups >> t-test -- >> even if >> you ave no evidence of a correlation between your pairs? Indeed you >> have >> evidence that the sample Pearson r should be set to zero, then the >> term >> - 2*r*SE1*SE2 in the denominator should be set to zero. If you do >> not >> set it >> to zero because you think that even without evidence of r > 0.00 you >> are >> "entitled" to do that version of the test, I'd really like to hear >> the >> justification >> and why it makes any sense instead of a misleading result. >> >> -Mike Palij >> New York University > >> mp26@ > >> >> ===================== >> To manage your subscription to SPSSX-L, send a message to > >> LISTSERV@.UGA > >> (not to SPSSX-L), with no body text except the >> command. To leave the list, send the command >> SIGNOFF SPSSX-L >> For a list of commands to manage subscriptions, send the command >> INFO REFCARD > > > > > > ----- > -- > Bruce Weaver > [hidden email] > http://sites.google.com/a/lakeheadu.ca/bweaver/ > > "When all else fails, RTFM." > > NOTE: My Hotmail account is not monitored regularly. > To send me an e-mail, please use the address shown above. > > -- > View this message in context: > http://spssx-discussion.1045642.n5.nabble.com/How-to-do-a-Ladder-graph-tp5731410p5731427.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except > the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
In reply to this post by Mike
I think you have two central problems. Your laxness on hypothesis testing. Your ignorance about intraclass correlations. I don't know if your cited text has the same problems, or if you are mis-reading. I haven't looked for your reference. If you are using him right, your source, Hoyle, is apparently much laxer than I am about the proper conclusions from "hypothesis testing." By my standard, the failure-to-reject does NOT affirm that the null is TRUE; rather, it states that there is insufficient evidence. I do agree that when you know that the elements are independent, it might be better to say that it is simply WRONG to set it up as a repeated-measure in the first place. I do not accept that "significance" is a proper guide for deciding on independence. (What I have read about the Mauchley test for sphericity stated that its power is so poor for small and medium n that -- instead of being guided by "0.05" -- one should probably use "0.5" unless your n's are really huge.) - see more comments inserted into the [stripped] text, below - > Date: Mon, 1 Feb 2016 23:21:56 -0500 > From: [hidden email] > Subject: Re: How to do a Ladder graph > To: [hidden email] > > ----- Original Message ----- > On Monday, February 01, 2016 8:44 PM,Rich Ulrich wortel > > > >Mostly, good and useful comments, but ... > > Thank you. However, some of the comments you make below > are unclear to me and perhaps you can clarify them a little > > Now, according to Hoyle, if the Pearson f is not significant > then the entire term -2*r*SE1*SE2 should be set to zero and > one is left with a version of the independent groups t-test. > But if one leaves that term while r is not significant, it will reduce > the > error variance (i.e, sum of VarErr1 + VarErr2)) and make the > donominator inappropriately smaller. How much of an effect > this has on the t-test depends upon how large the nonsignificant > - 2*r*SE1*SE2 is but it could provide seriously misleading > results. I can believe, "seriously /different/ results"; doubling the N changes the power of the t-test. The change in Mean-square matters more than the change in Sum-of-squares, if you are not otherwise noticing the d.f. I don't know if you are using Hoyle wrong; it sounds like he has it wrong. The paired t-test with n-1 d.f. is to be replaced by an independent- samples t-test with 2n-2 d.f. The difference in d.f. says that with the independent test, you are pretending to have twice the sample size; the error in this was implicit in my example of the "forced choice" with r nearly 1.0; you can prove that you have "too much power" if you let the sums total to 10, so that the correlation is perfect; and the independent test still pretends that the sample is twice as big as it actually is (that is, definitely "too much power" and the wrong test). - For r= 1.0, the one-sample test is, incontrovertibly, a proper test of the proper size. It is well known that a paired test, with a strong positive correlation, has much better power than the independent-samples test. It is less well recognized that a negative correlation has less power than the independent test; that certainly does NOT make it the preferred test - it makes it an improper test. [snip, more] > We've done this dance before ?? and simply put I doubt that Gosset/Student > or > Sir Ronald ever considered the case where measuring the same individual > twice would lead to a negative correlation because this occurs only in > rare situations. If the negative correlation is "real", then I think > one has a couple > of options: > (1) take the absolute value off the negative pearson r, do the > appropriate calculation, > and see if it make sense, - Now THAT is absolute nonsense. Negative correlations arise naturally for anything resembling an analysis of "compositions" that come to a fixed total (or near to one). - See my example of forced choice, time spent, analyzing (A, B) and dropping "indeterminate". I think Sir Roger would not be surprised or amazed. - Any analysis provided on rank-date (sum is fixed). - Geological assays show compositions that to 100% (or, nearly). - One early example that I read of was for the weights of a litter of certain lab-bred rats. The pups differ in weight, down to "runt"; the litters have exactly the same number of pups, and much more similarity in total weight that you would expect from the within-litter variance. The basic formula for intraclass correlation clearly allows for negative values; and they make good sense, both logically and analytically. Now, not all textbooks are always right. I heard a guest lecturer on campus a dozen years ago on Hierarchical Linear Models. He presented a formula for ICC which had to be positive. I raised the question about negative ICCs at the point where the last example clearly had a forcing situation where the ordinary ICC would be negative ... and the notion seemed new to the lecturer (whose name I forget). > or > (2) Make up you own damned test. If you have a pair of values x and y > on the same > individual, then Y would have to be blow the Y mean in order to obtain a > negative > correlation. Given that Gosset's concerns was with making sure that > contents of > vats of ale and stout did not vary significantly from vat to vat, I > think that Guinness > would have fired his ass if he ever obtain a negative correlation > between two measures > that should be the same. But I doubt that Gosset assumed that his laboratory represented the whole possible world of reasonable designs and hypotheses. -- Rich Ulrich |
|
Rich,
Just a couple of points::
(1) When one says "according to Hoyle" one is
using an old saying
that refers back to Edmond Hoyle's rules for
the playing of card games.
See:
Quoting: from the above source:
|The phrase "according to Hoyle" came into the language as a
|reflection of his generally perceived authority on the subject
So, when used in conversation, like I did
below, it meant "doing
things according to a recognized authority",
not some statistician
named Hoyle as you seem to have misunderstood.
See also:
I apologize for using pop culture refs that
you are unfamiliar with.
(2) Since Gosset worked for a Guinness
brewery, I don't believe
he worked in a lab, instead he probably worked
on measurements
taken by workers during the usual course of
brewing. If Guinness
was really concerned with lab work rather than
brewing beer, ale,
and stout, I don't think that Guinness
would have prevented their employees
from publishing papers with their real
names (hence "student" because Gosset
considered himself a lowly student compared to
his friend Sir Ronald).
Regarding negative correlations in t-tests and
other statistics that
typically assume positive correlations, I have
to admit that I have
never come across a situation in actual data
where this has occurred
without it being some sort of error. But
I am glad that you find the
topic interesting and I'm sure you are an
excellent resource about them.
But if I want advice about ICC's I'll ask
Pat Shrout about them.
NOTE: There are such things as negative
probabilities -- Feynman has
a chapter on them in the following
book:
and the Wikipedia has a kiiddie version of
their explanation; see:
Also, there is such a thing as "negative
temperature", that is,
temperature below absolute zero on the Kelvin
and related scales;
for the kiddie version of the explanation see
the Wikipedia entry:
I point these out just to say that just
because these negative entities exist,
I don't have to think about them -- I'm sure
there are others intensely
interested in them Similarly, for
negative correlations in situations where
they should be positive, I will leave it up to
you to worry about such
things because the phenomena I study do not
demonstrate them.
So, knock yourself out. And we'll
have to agree to disagree on the
other points (NOTE: a possible reference to "Men in Black
3").
-Mike Palij
New York University
===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
This has been discussed already, at length. The explanation I already provided a long time ago is below. ************************************* All, A comment was made regarding the possibility of fitting an incorrect variance-covariance structure, which could result in a negative variance component. While it is true that an incorrect variance-covariance could result in a negative variance component, it should be noted that, within a linear mixed model, often when this occurs, the variance-covariance structure is overly-complex given the data at hand. In fact, it is so common that some multilevel textbooks recommend that when a negative variance component is observed, simplification of the variance-covariance model be considered as the next logical step. However, if one fits a simple random intercept model, assuming a reasonably balanced design with adequate sample sizes at both levels, then the possibility does exist that the negative variance component is not only accurate, but interpretable. Moreover, if one forces the valid negative variance component to be zero (e.g. MIXED procedure in SPSS forces a random intercept to be non-negative), simulation studies have shown that the Type I Error Rate is inflated. OTOH, if one allows the variance component to be negative, the Type I Error Rate is maintained (reference: SAS for Mixed Models, 2nd ed., by Littell et al.). So, the question some might be pondering is...What type of naturally occurring environment would lead to a negative variance component? Littell et al. in SAS for mixed models (2nd ed.) discuss how a naturally competitive environment within a plot can result in a negative variance component. Competitive Environment Example: Suppose there are 50 cages, and within each of the 50 cages, 3 adult dogs of the same breed, health status, gender, age, and weight are placed in each cage on day 1. A single, large bowl of food of the same amount is placed in each cage every day for 30 days. Given that some dogs tend to be dominant while others tend to be submissive, would we be surprised to see a great deal of within-cage weight variability at the end of 30 days? Probably not. On the other hand, the means across the cages would be expected to be quite similar since the same amount of food had been placed in each cage every day. This could easily result in greater within-cage variability as compared to between-cage variability. Under such a scenario, it would not be surprising to obtain a negative between-cage variance component, and ultimately and negative intraclass correlation coefficient. (Note that this example was adapted from an example provided on SAS-L) Using the simulated example I provide BELOW, the between-cage variance component is -.310601. Interpretation: The between-cage variance is smaller than would be expected by a value of .310601. How do we calculate this value using data that is simulated from the code below? In addition to reading the output from the VARCOMP procedure or MIXED procedure (changing the structure from CSR to CS), we could subtract the between-cage variability that would be expected (within-subject variability / number of dogs per cage = 1.266169/3 = .422056) from the observed between cage variance (variance of cage means = .111455): between cage-variance component = .111455 - .422056 = .310601 Note: If we wanted to obtain the within-subject variability estimate (1.266169) without employing VARCOMP or MIXED, we could also use the MEANS procedure. Let's go a step further now and calculate the ICC (between-cage variance component) / (between-cage variance component + within-cage variance component) ICC = -.310601 / (-.310601 <a href="tel:+ 1.266169">+ 1.266169) = -.325043 Interpretation: This negative ICC reflects the within-cage correlation to be -.325043. Again, under a naturally competitive environment with a mix of dominant and submissive animals, would we be surprised to observe a negative within-cage correlation with respect to dog weight? Of course not! It makes perfect sense, and the model is deriving estimates that are interpretable. The information provided above comes directly from various sources, including messages posted on SAS-L over the years, along with a section in the book, SAS for Mixed Models, 2nd Edition, dedicated to interpreting negative variance components. I will admit that I was stuck trying to figure out the simulation code for quite a while, which delayed my posting this message. As some of you can tell, I prefer to provide simulated data to illustrate (and to some extent, validate) what I state. I was fortunate to obtain help creating the simulation code from someone off-list. I am grateful to that person. This can, at times, slow me down from responding to a message, but it's a preference of mine. Before I provide the code, I'd like to make one final comment. I understand how a negative variance component is disconcerting, to say the least. However, when interpreted correctly, it no longer seems problematic [to me]. For those who are uncomfortable observing negative variance components, there is an alternative parameterization that directly estimates the within-subject correlation! As you will see, the MIXED code below estimates the within-subject correlation under the compound-symmetric residual correlation structure. After employing the MIXED model, I take advantage of the VARCOMP procedure to estimate the negative variance component. Note that one could also simply change the residual variance-covariance structure in the MIXED code from CSR to CS to obtain the negative variance component. I will stop at this point and simply provide the code to estimate the model. Hope this is of interest to others. Ryan -- set seed 98734523. new file. inp pro. compute plot=-99. compute subject = -99. compute x1 = -99. compute x2 = -99. compute x3 = -99. compute e1 = -99. compute e2 = -99. compute e3 = -99. compute sigma = 1. compute rho = -0.35. compute a11 = 1. compute a21 = rho. compute a31 = rho. compute a22 = sqrt(1 - rho**2). compute a32 = (rho/(1+rho))*sqrt(1 - rho**2). compute a33 = sqrt(((1 - rho)*(1 + 2*rho))/(1 + rho)). leave plot to a33. loop plot= 1 to 50. compute x1 = rv.normal(0,1). compute x2 = rv.normal(0,1). compute x3 = rv.normal(0,1). compute e1 = sigma * a11*x1. compute e2 = sigma * (a21*x1 + a22*x2). compute e3 = sigma * (a31*x1 + a32*x2 + a33*x3). loop subject = 1 to 3. compute y = e1*(subject=1) + e2*(subject=2) + e3*(subject=3). end case. end loop. end loop. end file. end inp pro. exe. delete variables x1 x2 x3 sigma rho a11 a21 a31 a22 a32 a33 e1 e2 e3. MIXED y /FIXED= | SSTYPE(3) /METHOD=REML /PRINT=R SOLUTION /REPEATED=subject | SUBJECT(plot) COVTYPE(CSR). VARCOMP y BY plot /RANDOM=plot /METHOD=SSTYPE(3) /PRINT=SS /PRINT=EMS /DESIGN /INTERCEPT=INCLUDE. As you can see above, arriving at a negative ICC simply requires an understanding how a variance component and ICC are calculated. ************************************* I will not respond back to this post since all the proof necessary is right here, and this has already been discussed. Ryan ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
In reply to this post by Mike
Mike,
=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD
When I was writing three or four answers per day in the Usenet stats groups some years back, Reef Fish Bob asked me why I so often packaged my advice as, "in the applications that I know of" or "in biostatistics". My answer was something to the effect that I had already suffered falls from hubris a couple of times, when folks threw real examples at me that contradicted my too-narrow perspective. [RFBob was prone to make flat pronouncements that occasionally were wrong; he avoided embarrassment by never admitting he was wrong.] I even do assume that "small data sets used in textbooks" can have a real-world application, somewhere, even before I run into it. The questions about the limits are real questions to be aware of (and, sometimes, wary of). My "fish" data is not my invention; it was in a question that was posed (~2003) and I answered it. I was already familiar with the concept of "negative r" in a paired t. I remember, in particular, a question on an exam in my first year of grad school: 1) construct a small set of data for which the paired t will reject, and the independent t will not; 2) construct a set for which the independent t will reject and the paired test will not. Your formula for the error term (using r) gives the answer away. Our class had not been given that form of the formula, so it baffled everyone else and he omitted that Q from the scoring for the test. But I had read it in Fisher's book on experimental design, so it was obvious. Negative r, or negative ICC. Why does this rare-data circumstance matter? - Well, I think that if you intend to become a "real statistician" who understands his work, you will always want to figure out what makes the difference between any two competing tests. T-tests come pretty early in the curriculum. Sure, I'm familiar with "according to Hoyle." He was talking about card games, for which he documented the arbitrary rules. Your allusion was just too silly -- after all, this is science, and you are wrong -- for me to think that you didn't also have some authority: one who is wrong or who you persistently misread. I thought it was a clever word play ... not, what you seem to claim, that you were trying to push through your error by force of personality. After all, statistics are logical, and I had given you the logic where negative r's and ICCs make sense. Now, Ryan has, too, following the same not-so-unthinkable model of scores adding to a similar total. [Mike: But if I want advice about ICC's I'll ask Pat Shrout about them.] Please do that, if Pat is someone who can sort you out. -- Rich Ulrich Date: Thu, 4 Feb 2016 00:00:30 -0500 From: [hidden email] Subject: Re: How to do a Ladder graph To: [hidden email] Rich,
Just a couple of points::
(1) When one says "according to Hoyle" one is
using an old saying
that refers back to Edmond Hoyle's rules for
the playing of card games.
See: [ snip, irrelevancies; previous notes] |
|
In reply to this post by Mike
P.S.
=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD
Mike, I hold the same attitude towards negative /variances/ as what you suggest by your NOTE: on negative probabilities and negative absolute temperatures -- something exotic that I don't need to worry about. However, I think you are attributing the weirdness of "negative variance" to "negative correlations" and covariance. That is a huge error. Your own rejection of "real, negative r's" has already led you to deliver bad advice in this thread, so it should be a concern to you. IMO, "agree to disagree" properly applies to matters of opinion, not matters of fact. I have illustrated exactly how negative ICCs arise in several examples: by nature, by experimental design, and as a consequence of data manipulation (scores that total 100% or a nearly-fixed sum). -- Rich Ulrich Date: Thu, 4 Feb 2016 00:00:30 -0500 From: [hidden email] Subject: Re: How to do a Ladder graph To: [hidden email] Rich,
Just a couple of points::
. [snip, much] Regarding negative correlations in t-tests and other statistics that typically assume positive correlations, I have
to admit that I have
never come across a situation in actual data
where this has occurred
without it being some sort of error. But
I am glad that you find the
topic interesting and I'm sure you are an
excellent resource about them.
But if I want advice about ICC's I'll ask
Pat Shrout about them.
NOTE: There are such things as negative
probabilities -- Feynman has
a chapter on them in the following
book:
and the Wikipedia has a kiiddie version of
their explanation; see:
Also, there is such a thing as "negative
temperature", that is,
temperature below absolute zero on the Kelvin
and related scales;
for the kiddie version of the explanation see
the Wikipedia entry:
I point these out just to say that just
because these negative entities exist,
I don't have to think about them -- I'm sure
there are others intensely
interested in them Similarly, for
negative correlations in situations where
they should be positive, I will leave it up to
you to worry about such
things because the phenomena I study do not
demonstrate them.
So, knock yourself out. And we'll
have to agree to disagree on the
other points (NOTE: a possible reference to "Men in Black
3").
[snip] |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

