MANOVA
|
This post was updated on .
I want study the anxiety and depression scores in three types of pets with equal size ( 10 dogs, 10 cats and 10 hamsters). So we have here :
Independent variable : type of pet Dependent variables : Anxiety scores - Depression scores. I checked the following assumptions : - The correlation between the dependant variables because r = 0,30 - We have homogeneity of between-group for depression scores (siginficance>0,05), but not for anxiety scores in (siginficance<0,05) so I employ Brown-Forsythe and Welch's F test concerning anxiety. - We have homogeneity of variance-covariance matrices because Sig.>0,01, so the correlation between the dependant variables is equal across the groups. My questions : 1)- I know we can't choose Hotelling's Trace concerning F test but I read that Wilk's Lambda is the best choice even if Pillai's Trace is more powerful. But I don't know why we shouldn't choose Pillai's Trace or Roy's Largest Root F test? 2)- Concerning Post hoc test, I read that the best test for "Equal Variances Assumed" is Tukey, and for ""Equal Variances not Assumed" is Games-Howell. Why? 3)- I did the Brown-Forsythe and Welch's F test concerning anxiety : 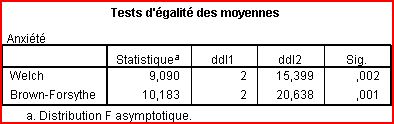 I read that "there is highly significant difference is anxiety scores across pet type " and I don't understand why? and that "The violation of homogeneity of variances poses no threat to the validity of our results" I don't undestand why? Thanks in advance :) |
|
Why are you interested in forming a weighted linear composite of the DVs? Why not perform separate univariate analyses?
Ryan > On Nov 29, 2013, at 12:09 AM, "Matthia's" <[hidden email]> wrote: > > I want study the anxiety and depression scores in three types of pets with > equal size ( 10 dogs, 10 cats and 10 hamsters). So we have here : > Independent variable : type of pet > Dependent variables : Anxiety scores - Depression scores. > > I checked the following assumptions : > - The correlation between the dependant variables because r = 0,30 > - We have homogeneity of between-group for depression scores > (siginficance>0,05), but not for anxiety scores in (siginficance<0,05) so I > employ Brown-Forsythe and Welch's F test concerning anxiety. > - We have homogeneity of variance-covariance matrices because Sig.>0,01, so > the correlation between the dependant variables is equal across the groups. > > My questions : > 1)- I know we can't choose Hotelling's Trace concerning F test but I read > that Wilk's Lambda is the best choice even if Pillai's Trace is more > powerful. But I don't know why we shouldn't choose Pillai's Trace or Roy's > Largest Root F test? > 2)- Concerning Post hoc test, I read that the best test for "Equal Variances > Assumed" is Tukey, and for ""Equal Variances not Assumed" is Games-Howell. > Why? > 3)- I did the Brown-Forsythe and Welch's F test concerning anxiety : > > I read that "there is highly significant difference is anxiety scores across > pet type " and I don't understand why? > and that "The violation of homogeneity of variances poses no threat to the > validity of our results" I don't undestand why? > > Thanks in advance :) > > > > -- > View this message in context: http://spssx-discussion.1045642.n5.nabble.com/MANOVA-tp5723364.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
|
Administrator
|
I've just searched the FM for "Brown-Forsythe", and the only place it appears is in the documentation for ONEWAY. So it would appear that the OP is in fact running univariate ANOVAs. This makes me think that they want the multivariate test as a preliminary omnibus test, presumably to control Type I error. If that is so, I suggest that the OP take a look at the classic article by Huberty & Morris (1989):
https://bitbucket.org/eyecat/readinglists/src/d8e8010f0b0d2dbb0863af3050411695254cc6b1/ReadingList_NotreDame/HubertyMorris1989MultivariateVsUnivariate.pdf Here is the first paragraph of the Discussion section: "Even though it is a fairly popular analysis route to take in the behavioral sciences, conducting a MANOVA as a preliminary step to multiple ANOVAS is not only unnecessary but irrelevant as well. We consider to be a myth the idea that one is controlling Type I error probability by following a significant MANOVA test with multiple ANOVA tests, each conducted using conventional significance levels. Furthermore, the research questions addressed by a MANOVA and by multiple ANOVAS are different; the results of one analysis may have little or no direct substantive bearing on the results of the other. To require MANOVA as a prerequisite of multiple ANOVAS is illogical, and the comfort of statistical protection is an illusion. The view that it is inappropriate to follow a significant MANOVA overall test with univariate tests is shared by others (e.g., Share, 1984)." Finally, with equal sample sizes, ANOVA is extremely robust to heterogeneity of variance. So I would not switch to the Welch or Brown-Forsythe F-tests simply because Levene's test is significant. Doing so will unnecessarily reduce power (by reducing the denominator df). HTH.
--
Bruce Weaver bweaver@lakeheadu.ca http://sites.google.com/a/lakeheadu.ca/bweaver/ "When all else fails, RTFM." PLEASE NOTE THE FOLLOWING: 1. My Hotmail account is not monitored regularly. To send me an e-mail, please use the address shown above. 2. The SPSSX Discussion forum on Nabble is no longer linked to the SPSSX-L listserv administered by UGA (https://listserv.uga.edu/). |
|
In reply to this post by Matthia's
See comments, interspersed.
> Date: Thu, 28 Nov 2013 21:09:38 -0800 > From: [hidden email] > Subject: MANOVA > To: [hidden email] > > I want study the anxiety and depression scores in three types of pets with > equal size ( 10 dogs, 10 cats and 10 hamsters). So we have here : > Independent variable : type of pet > Dependent variables : Anxiety scores - Depression scores. "Three types of pets" -- This is the definition of the universe being studied? With samples of 10 each, it seems that you might have descriptive study of "my own pets" or some such. I do know that dog breeds conventionally have different temperaments attributed to them. "Anxiety" and "depression" in animals is terminology that is evocative; the labels will be meet more approval from animal lovers than philosophers. I skip that issue, but raise the problem that psychologists once called "operationaizing." Surely this is from observing behavior. (Any other chance?) My own impression is that cats and dogs do differ in standard activities, but they are not usually locked in cages like the hamsters. It seems to me that the best you could hope to conclude from a study is that "These measurements do (or do not) give similar results when applied to pets in conditions of stress (or no stress)." In that case, showing the comparability is far more interesting that a weak (Ns of 10?) test. > > I checked the following assumptions : > - The correlation between the dependant variables because r = 0,30 > - We have homogeneity of between-group for depression scores > (siginficance>0,05), but not for anxiety scores in (siginficance<0,05) so I > employ Brown-Forsythe and Welch's F test concerning anxiety. > - We have homogeneity of variance-covariance matrices because Sig.>0,01, so > the correlation between the dependant variables is equal across the groups. You intend to conclude that var-cov matrices are equal "because Sig.> 0.01"? No. That is not a proper statement of what you can infer. You can, at best, say that "The matrices do not differ so much as to reject at the 1% level". With Ns of 10, that is a very weak claim. Anyway, if there are such differences, I fully expect them to owe to the weirdness of scaling or extreme scores in one group or another. For this pilot study of scaling across species, I would take seriously every piece of evidence of palpable difference. Thus, you might consider it a potential warning against the scaling if there is *any* evidence of heterogeneity, even at the 10% level. - On a further note: One should be very cautious about using tests of homogeneity as a preliminary for further testing. Essentially NO statisticians say that you should (for instance) decide which t-test to use, based on a test of variances. On the other hand, when doing Repeated Measures, the test of sphericity is so weak that you should be wary of a strong risk invalid comparisons whenever p< 0.50, not p< 0.05. > > My questions : > 1)- I know we can't choose Hotelling's Trace concerning F test but I read > that Wilk's Lambda is the best choice even if Pillai's Trace is more > powerful. But I don't know why we shouldn't choose Pillai's Trace or Roy's > Largest Root F test? The hypotheses tested in MANOVA are the set of "all possible combinations" of differences. I once included Anxiety and Depression and Psychoticism in a MANOVA because I wanted to test whether there was a different *pattern* showing in two groups of relapsers. (There was.) Usually, the interest in symptoms is one-sided: Are these people doing better than those people? - and the proper test is a composite score. Or, if you insisted on arbitrary weights, you might look at Roy's Largest Root instead of a predefined composite. However, given your circumstances of trying to show the equivalence (or not), your hypotheses deserve the more powerful and meaningful univariate examinations. No one should complain about "Too many tests" - you are not testing in that sort of circumstance. > 2)- Concerning Post hoc test, I read that the best test for "Equal Variances > Assumed" is Tukey, and for ""Equal Variances not Assumed" is Games-Howell. > Why? > 3)- I did the Brown-Forsythe and Welch's F test concerning anxiety : > > I read that "there is highly significant difference is anxiety scores across > pet type " and I don't understand why? Because the scales can't be applied across species, and still use the same norms? > and that "The violation of homogeneity of variances poses no threat to the > validity of our results" I don't undestand why? You don't say where you are reading that. Equal Ns make ANOVA very robust. Or maybe they also did the testing in another fashion to illustrate that? ... -- Rich Ulrich |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

