Weird distribution of regression weights after PCA
|
Hello.
I have 9 ordinal response variables (a questionnaire) and am performing a factor analysis. The variables are highly positively skewed, 40% have "0", 30 % "1", 20% "2" and 10% "3". Therefor, I cannot perform ML factor analysis and must use PCA, as far as I understand. Performing PCA (correlated factors) I find 2 strong factors (screeplot, Eigenvalue, R^2 all ok). I export regression weights now, and want to use these as new dependent variables in subsequent analyses. If I run frequencies on these 2 new variables, not only are they very positively skewed, but there are certain values that are plain weird. I have N=3000, and nearly all values of these new variables have N=1 or N=2 in the frequencies. However, there are 4 values on which 5-10% of the population converge! Attached a screenshot of a part of the frequency table (see the 13% value!). 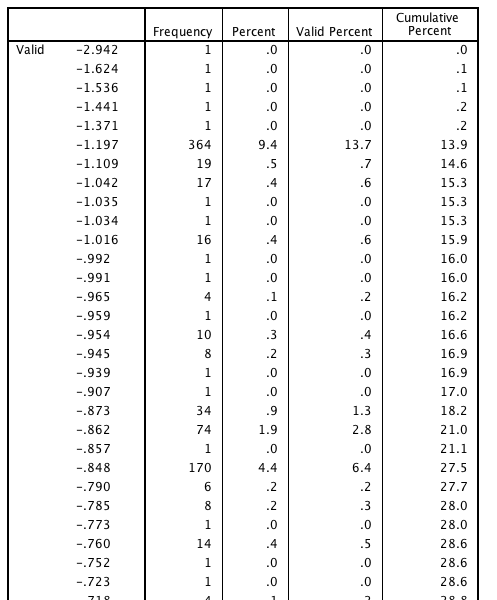 What could be the cause for this? Thanks T |
Re: Weird distribution of regression weights after PCA
|
Administrator
|
I will refrain from comment on the appropriateness of PCA on highly skewed 4 category ordinal data ;-)
I will however direct you to SORT on your 'factor scores' and look at the values of the 9 variables where the value is dense ie '??converged??'. Hmmmmm....I surmise that each of those cases with an identical 'score' have the **same** profile on the input variables. Will leave that to you to puzzle out! ESP? Nah, common sense!!! ---
Please reply to the list and not to my personal email.
Those desiring my consulting or training services please feel free to email me. --- "Nolite dare sanctum canibus neque mittatis margaritas vestras ante porcos ne forte conculcent eas pedibus suis." Cum es damnatorum possederunt porcos iens ut salire off sanguinum cliff in abyssum?" |
Re: Weird distribution of regression weights after PCA
|
In reply to this post by torvon
Did you try CATPCA? Did the level of measure make a
substantive difference?
Did you do a parallel analysis to ballpark your stopping rule? How many constructs were the responses variables designed to measure? What happens if you use one/zero weights to get the scores? Did you eliminate items that did not load cleanly do that you had divergent validity? What does the internal consistency of the scores look like? Do the resulting scales make sense as constructs? How did you get the set of response variables? Art Kendall Social Research Consultants On 5/8/2012 10:41 AM, torvon wrote: ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARDHello. I have 9 ordinal response variables (a questionnaire) and am performing a factor analysis. The variables are highly positively skewed, 40% have "0", 30 % "1", 20% "2" and 10% "3". Therefor, I cannot perform ML factor analysis and must use PCA, as far as I understand. Performing PCA (correlated factors) I find 2 strong factors (screeplot, Eigenvalue, R^2 all ok). I export regression weights now, and want to use these as new dependent variables in subsequent analyses. If I run frequencies on these 2 new variables, not only are they very positively skewed, but there are certain values that are plain weird. I have N=3000, and nearly all values of these new variables have N=1 or N=2 in the frequencies. However, there are 4 values on which 5-10% of the population converge! Attached a screenshot of a part of the frequency table (see the 13% value!). http://spssx-discussion.1045642.n5.nabble.com/file/n5694967/frequencies.png What could be the cause for this? Thanks T -- View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Weird-distribution-of-regression-weights-after-PCA-tp5694967.html Sent from the SPSSX Discussion mailing list archive at Nabble.com. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD
Art Kendall
Social Research Consultants |
Re: Weird distribution of regression weights after PCA
|
Administrator
|
In reply to this post by David Marso
An illustration of the point(s) I was making below.
INPUT PROGRAM. - LOOP I=1 TO 3000. + COMPUTE Eta1=UNIFORM(10). + COMPUTE Eta2=UNIFORM(10). - DO REPEAT Y=Y1 TO Y9 / F1=.8 .8 .8 .8 .8 .2 .2 .2 .2 / F2=.2 .2 .2 .2 .2 .8 .8 .8 .8. + COMPUTE Y = RND((F1*Eta1 + F2*Eta2 + Uniform(1))/3). - END REPEAT. + END CASE. - END LOOP. END FILE. END INPUT PROGRAM. ****----------------------------***. FACTOR /VARIABLES y1 y2 y3 y4 y5 y6 y7 y8 y9 /ROTATION VARIMAX/SAVE REG(ALL). ** Notice R(1-5:1-5) , R(1:5,Eta1), R(6-9:Eta2), R(6-9:6-9) R(Eta1,fac_1_1), R(Eta2,fac2_1) high ** R(1-5:6-9) R(Eta1:Eta2) etc....... low *******. CORRELATIONS /VARIABLES=eta1 fac1_1 eta2 fac2_1 y1 y2 y3 y4 y5 y6 y7 y8 y9 . ** See how the FREQS are the **SAME** for the top several values for both fac1_1 and fac2_1. FREQUENCIES VARIABLES=fac1_1 fac2_1/FORMAT DFREQ. REG DEP fac1_1 / METHOD ENTER y1 TO y9. REG DEP fac2_1 / METHOD ENTER y1 TO y9. SORT CASES BY fac1_1 fac2_1. AGGREGATE OUTFILE 'tmp' / BREAK fac1_1 fac2_1/ N=N. MATCH FILES / FILE * / TABLE 'tmp' / BY fac1_1 fac2_1 . ** Now inspect the response patterns for the modal factor score values!! IDENTICAL **. SORT CASES BY N (D).
Please reply to the list and not to my personal email.
Those desiring my consulting or training services please feel free to email me. --- "Nolite dare sanctum canibus neque mittatis margaritas vestras ante porcos ne forte conculcent eas pedibus suis." Cum es damnatorum possederunt porcos iens ut salire off sanguinum cliff in abyssum?" |
|
Thank you for the input.
The difficulty is that CATPCA can extract two factors, with similar Eigenvalues like FACTOR, but the loadings are very differently. CATPCA clearly favors a 1 factor solution (mostly because the reliability of the second factor is abysmal with cronbach alpha of -0.05), whereas FACTOR clearly favors a 2 factor solution. What I don't understand is that a CFA in MPLUS shows better fit for a 2 factor solution! Is there a way to run a COMMON FACTOR ANALYSIS in SPSS - not just a PCA? I read that one should use the polychoric correlation matrix as basis for modeling ordinal CFA and found a paper trying to implement R code in SPSS for this (M. Zack kindly provided me with the paper). "How many constructs were the responses variables designed to measure?" There is a lot of discussion about this. It was designed to measure 1 construct, but people keep finding 2 latent factors. That is why I would like to use a real common factor analysis, not a PCA, which is not really suitable to find latent factors. "What does the internal consistency of the scores look like?" Good for 1 factor - .85. Good for 2 factors in FACTOR, abysmal in 2 factors in CATPCA (first factor .9, second -.05). "Do the resulting scales make sense as constructs?" Yes. |
Re: Weird distribution of regression weights after PCA
|
Administrator
|
"Is there a way to run a COMMON FACTOR ANALYSIS in SPSS - not just a PCA?"
SPSS allows you to specify several methods for factor extraction. Principal Axis Factor (PAF) is what is commonly referred to as "Common Factor Analysis". --
Please reply to the list and not to my personal email.
Those desiring my consulting or training services please feel free to email me. --- "Nolite dare sanctum canibus neque mittatis margaritas vestras ante porcos ne forte conculcent eas pedibus suis." Cum es damnatorum possederunt porcos iens ut salire off sanguinum cliff in abyssum?" |
Re: Weird distribution of regression weights after PCA
|
In reply to this post by torvon
Did you use RELIABILITY to get the Cronbach's alpha?
Did you reflect items with negative loadings?
What does the "alpha if item deleted" column show? are there negative interitem correlations in the RELIABILITY output? Did you keep only clean loading items in the scoring key? A good set of items should have some positively loading and some negatively loading items. The negatively loading items are reflected for RELIABILITY and for the scoring key. Do the CATPCA loadings result in the same scoring key as FACTOR? Check the documentation for CATPCA to see if you need to reflect some items before CATPCA. What syntax are you using for FACTOR? Common factor analysis uses the principal axes method which puts squared multiple correlation coefficients in the diagonal of the matrix. In other words unique item variance is pooled with error variance. Only the common variance is considered a repeated measure of the construct. What syntax did you use for the Factor analysis? Did you use varimax rotation to maximize discriminant validity? How do your eigenvalues compare to those from a parallel analysis? Art Kendall Social Research Consultants On 5/12/2012 6:41 AM, torvon wrote: ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARDThank you for the input. The difficulty is that CATPCA can extract two factors, with similar Eigenvalues like FACTOR, but the loadings are very differently. CATPCA clearly favors a 1 factor solution (mostly because the reliability of the second factor is abysmal with cronbach alpha of -0.05), whereas FACTOR clearly favors a 2 factor solution. What I don't understand is that a CFA in MPLUS shows better fit for a 2 factor solution! Is there a way to run a COMMON FACTOR ANALYSIS in SPSS - not just a PCA? I read that one should use the polychoric correlation matrix as basis for modeling ordinal CFA and found a paper trying to implement R code in SPSS for this (M. Zack kindly provided me with the paper). "How many constructs were the responses variables designed to measure?" There is a lot of discussion about this. It was designed to measure 1 construct, but people keep finding 2 latent factors. That is why I would like to use a real common factor analysis, not a PCA, which is not really suitable to find latent factors. "What does the internal consistency of the scores look like?" Good for 1 factor - .85. Good for 2 factors in FACTOR, abysmal in 2 factors in CATPCA (first factor .9, second -.05). "Do the resulting scales make sense as constructs?" Yes. -- View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Weird-distribution-of-regression-weights-after-PCA-tp5694967p5706951.html Sent from the SPSSX Discussion mailing list archive at Nabble.com. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD
Art Kendall
Social Research Consultants |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |


