logistic regression interaction
|
Hello,
I am specifying a logistic regression model with an interaction between two categorical variables-social class and whether the person works shifts. The interaction increases model fit and is substantively meaningful so want to include it in my presentation of findings. Just so you understand what I mean, these are the odds ratios for the model: Social Class Managerial (ref) Intermediate 3.30* Routine 4.13* ShiftWork Yes (ref) No 1.17 Interaction Managerial/ShiftWork (ref) Intermediate/Shiftwork 8.04* Routine/Shiftwork 3.46* Now I want to present a 6 category table illustrating the interaction odd ratios only for all combinations of shiftwork social class. I have been reading the Jaccard book but am thinking I have been doing interactions like this one incorrectly and am currently slightly confused so any help would be appreciated: Is there a way I can get the rest of the interaction odds ratios by hand (not with SPSS) by the output I have already from running the model and is there a relatively simple way to get confidence intervals for the new terms? I am particularly interested in CI calculation. Many thanks, Anna |
|
Anna,
There are a couple of ways to achieve what you desire. One way would be to fit the logistic regression model employing the GENLIN procedure. Request that the procedure output the estimated marginal means for the interaction term (for the linear predictor). You'll see that those estimates are the log odds for every possible combination of Factors A and B, along with 95% CIs. Exponentiate the esimated log odds (including the lower and upper limit estimates, of course) and you're all set. To provide you with a concrete example, I generate data below and then fit the model using the GENLIN procedure. Ryan -- *Generate Data. set seed 98765432. new file. inp pro. loop ID= 1 to 10000. comp FactorA = rv.bernoulli(0.5). comp FactorB = rv.bernoulli(0.5). comp b0 = -1.5. comp b1 = 0.9. comp b2 = 0.5. comp b3 = 1.2. comp eta = b0 + b1*FactorA + b2*FactorB + b3*FactorA*FactorB. comp prob = exp(eta) / (1+ exp(eta)). comp y = rv.bernoulli(prob). end case. end loop. end file. end inp pro. exe. Delete variables b0 b1 b2 b3 eta prob. *Fit the model. GENLIN y (REFERENCE=FIRST) BY FactorA FactorB (ORDER=DESCENDING) /MODEL FactorA FactorB FactorA*FactorB INTERCEPT=YES DISTRIBUTION=BINOMIAL LINK=LOGIT /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED /MISSING CLASSMISSING=EXCLUDE /PRINT CPS DESCRIPTIVES MODELINFO FIT SUMMARY SOLUTION. On Sat, Aug 14, 2010 at 4:50 AM, annastella <[hidden email]> wrote: > Hello, > > I am specifying a logistic regression model with an interaction between two > categorical variables-social class and whether the person works shifts. The > interaction increases model fit and is substantively meaningful so want to > include it in my presentation of findings. > > Just so you understand what I mean, these are the odds ratios for the model: > > Social Class > Managerial (ref) > Intermediate 3.30* > Routine 4.13* > > ShiftWork > Yes (ref) > No 1.17 > > Interaction > Managerial/ShiftWork (ref) > Intermediate/Shiftwork 8.04* > Routine/Shiftwork 3.46* > > Now I want to present a 6 category table illustrating the interaction odd > ratios only for all combinations of shiftwork social class. > I have been reading the Jaccard book but am thinking I have been doing > interactions like this one incorrectly and am currently slightly confused so > any help would be appreciated: Is there a way I can get the rest of the > interaction odds ratios by hand (not with SPSS) by the output I have already > from running the model and is there a relatively simple way to get > confidence intervals for the new terms? I am particularly interested in CI > calculation. > > Many thanks, > > Anna > > > > > -- > View this message in context: http://spssx-discussion.1045642.n5.nabble.com/logistic-regression-interaction-tp2635146p2635146.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD > ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: logistic regression interaction
|
Hi Ryan,
Thanks a lot for that-will have a go with it and see what it gives me. However, may I ask if you or anyone knows a way to calculate the odds ratios (not the CIs necessarily) for the categories missing in the output (i.e. 3 social class groups for non shift-workers)? Not in terms of syntax really, just want to see I understand the interaction calculation right while working this out. Many thanks Anna |
|
Anna,
To answer your question, we need to write out the equation, and to write out the equation we need to have common language: If you have two categorical independent variables (Factor A has two levels and Factor B has 3 levels), then let A2 be the indicator of Factor A and B2 and B3 be the indicators of Factor B. The first levels of Factor A and B are the reference groups. Lower case letters denote coefficients. Equation: logit(y) = m + a2*A2 + b2*B2 + b3*B3 + ab22*A2*B2 + ab23*A2*B3 Then, Odds|(A=1,B=1) = exp(m) Odds|(A=1,B=2) = exp(m + b2) Odds|(A=1,B=3) = exp(m + b3) Odds|(A=2,B=2) = exp(m + a2 + b2 + ab22) Odds|(A=2,B=3) = exp(m + a2 + b3 + ab23) Ryan On Sat, Aug 14, 2010 at 5:04 PM, annastella <[hidden email]> wrote: > Hi Ryan, > > Thanks a lot for that-will have a go with it and see what it gives me. > > However, may I ask if you or anyone knows a way to calculate the odds ratios > (not the CIs necessarily) for the categories missing in the output (i.e. 3 > social class groups for non shift-workers)? Not in terms of syntax really, > just want to see I understand the interaction calculation right while > working this out. > > Many thanks > Anna > -- > View this message in context: http://spssx-discussion.1045642.n5.nabble.com/logistic-regression-interaction-tp2635146p2635437.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD > ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: logistic regression interaction
|
Ryan's approach is excellent in tehms of understanding the model and
process. If you are just looking to get the values for the unlisted categories, the easieest way is to just switch reference categories. If you are using default indicator coding then the last category is the reference and it has an OR=1.0. If you specify the first category as the reference you will get an OR for the last category in the output the is the OR for the last category relative to the first. If you are using deviation contrasts, then the missing category OR is obtained by merely changing the reference from the defualt to first. This can be doen with menus. If you would like a category other than first or last to be used in any type of contrast coding, use syntax and change it the the desired referecne category level and rerun fro mthe syntax window. MK ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: logistic regression interaction
|
In reply to this post by annastella
annastella wrote:
> I am specifying a logistic regression model with an interaction > between two categorical variables-social class and whether the person > works shifts. The interaction increases model fit and is > substantively meaningful so want to include it in my presentation of > findings. I wrote a webpage at my old website about interactions in logistic regression that you may find helpful: * http://www.childrensmercy.org/stats/weblog2004/interactions.asp --- Steve Simon, Standard Disclaimer Sign up at www.pmean.com/news for The Monthly Mean, the newsletter that dares to call itself average. ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
Re: logistic regression interaction --- computing CIs for Odds Ratios (ORs)
|
In reply to this post by Ryan
Hello Ryan and other contributors,
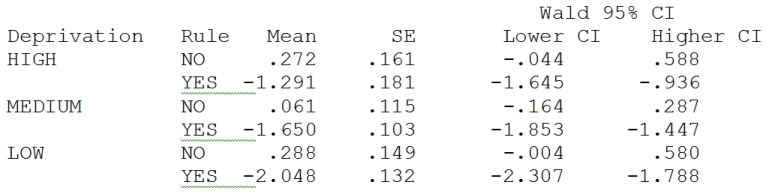
I have a question similar to the one asked by anastella, but would like to get ODDS RATIOS (ORs) with confidence intervals (CIs). My interaction is a 2 X 3 (exposed/not exposed to a rule X 3 levels of material deprivation [high – medium – low]). The outcome of interest is exposure to cigarette smoke. With GENLIN, I get log odds for the 6 combinations. I used the /EMMEANS TABLES = FactorA*FactorB SCALE = TRANSFORMED syntax that Ryan suggested.
Here’s what I get:
Wald 95% CI
Deprivation Rule Mean SE Lower CI Higher CI
HIGH NO .272 .161 -.044 .588
YES -1.291 .181 -1.645 -.936
MEDIUM NO .061 .115 -.164 .287
YES -1.650 .103 -1.853 -1.447
LOW NO .288 .149 -.004 .580
YES -2.048 .132 -2.307 -1.788
If I apply exp(log odds) to the column “Mean”, I understand that I will get ODDS. For example:
exp(.272) = 1.313 (odds of the outcome for high deprivation & rule=NO) and exp(-1.291) = 0.275 (odds for high deprivation & rule=YES).
Therefore, OR = exp(.272)/exp(-1.291) = 1.313 / 0.275 = 4.774
This indicates that the odds of being exposed to cigarette smoke in the high deprivation group is approximately 5 times higher among those without a rule when compared to those with a rule.
I am however unable to get the correct 95% CI for this OR. I am quite sure the answer is straightforward, but I do not get it.
When I apply the same computation as presented above to the Lower CI and Higher CI, it doesn’t work.
Many thanks in advance for your help.
Michael
|
Re: logistic regression interaction --- computing CIs for Odds Ratios (ORs)
|
I apologize... my text was not properly formatted. In order to facilitate the reading of my results, I included an image with the data.
---- Hi Ryan and other contributors, I have a question similar to the one asked by anastella, but would like to get ODDS RATIOS (ORs) with confidence intervals (CIs). My interaction is a 2 X 3 (exposed/not exposed to a rule X 3 levels of material deprivation [high – medium – low]). The outcome of interest is exposure to cigarette smoke. With GENLIN, I get log odds for the 6 combinations. I used the /EMMEANS TABLES = FactorA*FactorB SCALE = TRANSFORMED syntax that Ryan suggested. Here’s what I get:
Therefore, OR = exp(.272)/exp(-1.291) = 1.313 / 0.275 = 4.774 This indicates that the odds of being exposed to cigarette smoke in the high deprivation group is approximately 5 times higher among those without a rule when compared to those with a rule. I am however unable to get the correct 95% CI for this OR. I am quite sure the answer is straightforward, but I do not get it. When I apply the same computation as presented above to the Lower CI and Higher CI, it doesn’t work. Many thanks in advance for your help. Michael |
Re: logistic regression interaction
|
Administrator
|
In reply to this post by Ryan
This is a great approach for dealing with the interaction of two categorical variables. I would suggest just one small change to Ryan's GENLIN command: I.e., if you add COMPARE on the EMMEANS sub-command, you will get the log(odds ratios) with 95% confidence intervals--and these can be exponentiated to get odds ratios. E.g.,
*Fit the model. GENLIN y (REFERENCE=FIRST) BY FactorA FactorB (ORDER=DESCENDING) /MODEL FactorA FactorB FactorA*FactorB INTERCEPT=YES DISTRIBUTION=BINOMIAL LINK=LOGIT /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED compare=FactorA /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED compare=FactorB /MISSING CLASSMISSING=EXCLUDE /PRINT CPS DESCRIPTIVES MODELINFO FIT SUMMARY SOLUTION. HTH.
--
Bruce Weaver bweaver@lakeheadu.ca http://sites.google.com/a/lakeheadu.ca/bweaver/ "When all else fails, RTFM." PLEASE NOTE THE FOLLOWING: 1. My Hotmail account is not monitored regularly. To send me an e-mail, please use the address shown above. 2. The SPSSX Discussion forum on Nabble is no longer linked to the SPSSX-L listserv administered by UGA (https://listserv.uga.edu/). |
|
This thread is pretty old at this point, but from what I remember,
Anna was interested in obtaining the odds for each possible combination. That's why I suggested the EMMEANS statement without the COMPARE option. Ryan On Tue, Apr 19, 2011 at 5:40 PM, Bruce Weaver <[hidden email]> wrote: > This is a great approach for dealing with the interaction of two categorical > variables. I would suggest just one small change to Ryan's GENLIN command: > I.e., if you add COMPARE on the EMMEANS sub-command, you will get the > log(odds ratios) with 95% confidence intervals--and these can be > exponentiated to get odds ratios. E.g., > > *Fit the model. > GENLIN y (REFERENCE=FIRST) BY FactorA FactorB (ORDER=DESCENDING) > /MODEL FactorA FactorB FactorA*FactorB INTERCEPT=YES > DISTRIBUTION=BINOMIAL LINK=LOGIT > /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED compare=FactorA > /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED compare=FactorB > /MISSING CLASSMISSING=EXCLUDE > /PRINT CPS DESCRIPTIVES MODELINFO FIT SUMMARY SOLUTION. > > > HTH. > > > > R B wrote: >> >> Anna, >> >> There are a couple of ways to achieve what you desire. One way would >> be to fit the logistic regression model employing the GENLIN >> procedure. Request that the procedure output the estimated marginal >> means for the interaction term (for the linear predictor). You'll see >> that those estimates are the log odds for every possible combination >> of Factors A and B, along with 95% CIs. Exponentiate the esimated log >> odds (including the lower and upper limit estimates, of course) and >> you're all set. >> >> To provide you with a concrete example, I generate data below and then >> fit the model using the GENLIN procedure. >> >> Ryan >> -- >> >> *Generate Data. >> >> set seed 98765432. >> new file. >> >> inp pro. >> >> loop ID= 1 to 10000. >> >> comp FactorA = rv.bernoulli(0.5). >> comp FactorB = rv.bernoulli(0.5). >> comp b0 = -1.5. >> comp b1 = 0.9. >> comp b2 = 0.5. >> comp b3 = 1.2. >> comp eta = b0 + b1*FactorA + b2*FactorB + b3*FactorA*FactorB. >> comp prob = exp(eta) / (1+ exp(eta)). >> >> comp y = rv.bernoulli(prob). >> >> end case. >> end loop. >> end file. >> end inp pro. >> exe. >> >> Delete variables b0 b1 b2 b3 eta prob. >> >> *Fit the model. >> GENLIN y (REFERENCE=FIRST) BY FactorA FactorB (ORDER=DESCENDING) >> /MODEL FactorA FactorB FactorA*FactorB INTERCEPT=YES >> DISTRIBUTION=BINOMIAL LINK=LOGIT >> /EMMEANS TABLES=FactorA*FactorB SCALE=TRANSFORMED >> /MISSING CLASSMISSING=EXCLUDE >> /PRINT CPS DESCRIPTIVES MODELINFO FIT SUMMARY SOLUTION. >> >> >> On Sat, Aug 14, 2010 at 4:50 AM, annastella <[hidden email]> >> wrote: >>> Hello, >>> >>> I am specifying a logistic regression model with an interaction between >>> two >>> categorical variables-social class and whether the person works shifts. >>> The >>> interaction increases model fit and is substantively meaningful so want >>> to >>> include it in my presentation of findings. >>> >>> Just so you understand what I mean, these are the odds ratios for the >>> model: >>> >>> Social Class >>> Managerial (ref) >>> Intermediate 3.30* >>> Routine 4.13* >>> >>> ShiftWork >>> Yes (ref) >>> No 1.17 >>> >>> Interaction >>> Managerial/ShiftWork (ref) >>> Intermediate/Shiftwork 8.04* >>> Routine/Shiftwork 3.46* >>> >>> Now I want to present a 6 category table illustrating the interaction odd >>> ratios only for all combinations of shiftwork social class. >>> I have been reading the Jaccard book but am thinking I have been doing >>> interactions like this one incorrectly and am currently slightly confused >>> so >>> any help would be appreciated: Is there a way I can get the rest of the >>> interaction odds ratios by hand (not with SPSS) by the output I have >>> already >>> from running the model and is there a relatively simple way to get >>> confidence intervals for the new terms? I am particularly interested in >>> CI >>> calculation. >>> >>> Many thanks, >>> >>> Anna >>> >>> >>> >>> >>> -- >>> View this message in context: >>> http://spssx-discussion.1045642.n5.nabble.com/logistic-regression-interaction-tp2635146p2635146.html >>> Sent from the SPSSX Discussion mailing list archive at Nabble.com. >>> >>> ===================== >>> To manage your subscription to SPSSX-L, send a message to >>> [hidden email] (not to SPSSX-L), with no body text except the >>> command. To leave the list, send the command >>> SIGNOFF SPSSX-L >>> For a list of commands to manage subscriptions, send the command >>> INFO REFCARD >>> >> >> ===================== >> To manage your subscription to SPSSX-L, send a message to >> [hidden email] (not to SPSSX-L), with no body text except the >> command. To leave the list, send the command >> SIGNOFF SPSSX-L >> For a list of commands to manage subscriptions, send the command >> INFO REFCARD >> > > > ----- > -- > Bruce Weaver > [hidden email] > http://sites.google.com/a/lakeheadu.ca/bweaver/ > > "When all else fails, RTFM." > > NOTE: My Hotmail account is not monitored regularly. > To send me an e-mail, please use the address shown above. > > -- > View this message in context: http://spssx-discussion.1045642.n5.nabble.com/logistic-regression-interaction-tp2635146p4314424.html > Sent from the SPSSX Discussion mailing list archive at Nabble.com. > > ===================== > To manage your subscription to SPSSX-L, send a message to > [hidden email] (not to SPSSX-L), with no body text except the > command. To leave the list, send the command > SIGNOFF SPSSX-L > For a list of commands to manage subscriptions, send the command > INFO REFCARD > ===================== To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD |
«
Return to SPSSX Discussion
|
1 view|%1 views
| Free forum by Nabble | Edit this page |