Deriving Formula from Ordinal Regression Results to Classify New Cases?

[Vik Rubenfeld]

Hi Clare, Eugene,

Per Clare:

> Y= a+b1X1+b2X2+..

Per Eugene:

>The “y” that is computed is the log odds. I’d think you want to know whether the probability of being in
>the comparison group is greater than 0.5. If so there are a couple of other computational steps.

Would it be correct to compute Y, using the formula provided by Clare, for each possible value of the DV, and then to select the value with the highest Y as the predicted value for the DV?

Best,


-Vik

>
>On Oct 24, 2012, at 7:03 AM, Maguin, Eugene wrote:
>
>I may be misunderstanding some things but …
>
>The “y” that is computed is the log odds. I’d think you want to
>know whether the probability of being in the comparison group is
>greater than 0.5. If so there are a couple of other computational
>steps.
>
>Gene Maguin
>
>
>From: SPSSX(r) Discussion [mailto:[e-mail]] On
>Behalf Of Yifan Lu Sent: Wednesday, October 24, 2012 9:11 AM To:
>[e-mail] Subject: Re: Deriving Formula from
>Ordinal Regression Results to Classify New Cases?
>
>Hi Vik,
>
>I just did some similar work recently. Basically once you have
>output from an Ordinal Regression, write down the formula in Y=
>a+b1X1+b2X2+...you should know a and bi from your output. Then
>use this formula in your excel sheet as a simulation model in
>excel, with X1, X2...as independent variables for clients to
>enter. Y is the predicted value.
>
>Hope this helps.
>
>Clare
>
>From: SPSSX(r) Discussion on behalf of Vik Rubenfeld Sent: Tue
>10/23/2012 8:30 PM To: [e-mail] Subject: Deriving
>Formula from Ordinal Regression Results to Classify New Cases?
>
>What is the correct method for deriving a formula from the
>results of an Ordinal Regression, that can be used to predict the
>value of the dependent variable for new cases?
>
>Thanks very much in advance to all for any info.
>
>Best,
>
>
>-Vik

[Maguin, Eugene]

My understanding is this: It's not the highest value per se. The computed value is the log odds and you get one computed value for each level of the DV excluding the reference level. Exponentiate those values to get the odds. Then compute the probablility for each level. The formula is, I think, (odds/(1+odds)). You will see one two results: 1) none of the computed probabilities are greater than 0.5. Therefore the case goes in the reference group. 2) One of the computed probabilities is greater than 0.5. Therefore the case goes in that group. Can two or more of the computed probabilities be greater than 0.5?? I don't have enough experience to say. There's others on the list that know a lot more about this than I do. Perhaps they will comment.

Gene Maguin

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of Vik Rubenfeld
Sent: Wednesday, October 24, 2012 2:19 PM
To: [hidden email]
Subject: Deriving Formula from Ordinal Regression Results to Classify New Cases?

Hi Clare, Eugene,

Per Clare:

> Y= a+b1X1+b2X2+..

Per Eugene:

>The “y” that is computed is the log odds. I’d think you want to know
whether the probability of being in
>the comparison group is greater than 0.5. If so there are a couple of
>other
computational steps.

Would it be correct to compute Y, using the formula provided by Clare, for each possible value of the DV, and then to select the value with the highest Y as the predicted value for the DV?

Best,


-Vik

>
>On Oct 24, 2012, at 7:03 AM, Maguin, Eugene wrote:
>
>I may be misunderstanding some things but …
>
>The “y” that is computed is the log odds. I’d think you want to know
>whether the probability of being in the comparison group is greater
>than 0.5. If so there are a couple of other computational steps.
>
>Gene Maguin
>
>
>From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf
>Of Yifan Lu Sent: Wednesday, October 24, 2012 9:11 AM To:
>[hidden email] Subject: Re: Deriving Formula from Ordinal
>Regression Results to Classify New Cases?
>
>Hi Vik,
>
>I just did some similar work recently. Basically once you have output
>from an Ordinal Regression, write down the formula in Y=
>a+b1X1+b2X2+...you should know a and bi from your output. Then
>use this formula in your excel sheet as a simulation model in excel,
>with X1, X2...as independent variables for clients to enter. Y is the
>predicted value.
>
>Hope this helps.
>
>Clare
>
>From: SPSSX(r) Discussion on behalf of Vik Rubenfeld Sent: Tue
>10/23/2012 8:30 PM To: [hidden email] Subject: Deriving
>Formula from Ordinal Regression Results to Classify New Cases?
>
>What is the correct method for deriving a formula from the results of
>an Ordinal Regression, that can be used to predict the value of the
>dependent variable for new cases?
>
>Thanks very much in advance to all for any info.
>
>Best,
>
>
>-Vik

--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[David Marso]

It would also be useful to know which SPSS procedure is to be used for the analysis.
IIRC SPSS has NOMREG, PLUM , GENLIN and maybe others (hard to keep track of all the players) which handle Nominal Response variables.   Do each of these always result in the same results?  It would be interesting to know how to ensure that the client is aware of the various assumptions and how to not end up with GIGO by doing something unanticipated/off the reservation.  I imagine things will really get dicey when you start trying to build Excel spreadsheets which are also smart about categorical predictors and say interactions...;-))
---

Maguin, Eugene wrote

My understanding is this: It's not the highest value per se. The computed value is the log odds and you get one computed value for each level of the DV excluding the reference level. Exponentiate those values to get the odds. Then compute the probablility for each level. The formula is, I think, (odds/(1+odds)). You will see one two results: 1) none of the computed probabilities are greater than 0.5. Therefore the case goes in the reference group. 2) One of the computed probabilities is greater than 0.5. Therefore the case goes in that group. Can two or more of the computed probabilities be greater than 0.5?? I don't have enough experience to say. There's others on the list that know a lot more about this than I do. Perhaps they will comment.

Gene Maguin

-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of Vik Rubenfeld
Sent: Wednesday, October 24, 2012 2:19 PM
To: [hidden email]
Subject: Deriving Formula from Ordinal Regression Results to Classify New Cases?

Hi Clare, Eugene,

Per Clare:

> Y= a+b1X1+b2X2+..

Per Eugene:

>The “y” that is computed is the log odds. I’d think you want to know
whether the probability of being in
>the comparison group is greater than 0.5. If so there are a couple of
>other
computational steps.

Would it be correct to compute Y, using the formula provided by Clare, for each possible value of the DV, and then to select the value with the highest Y as the predicted value for the DV?

Best,


-Vik

>
>On Oct 24, 2012, at 7:03 AM, Maguin, Eugene wrote:
>
>I may be misunderstanding some things but …
>
>The “y” that is computed is the log odds. I’d think you want to know
>whether the probability of being in the comparison group is greater
>than 0.5. If so there are a couple of other computational steps.
>
>Gene Maguin
>
>
>From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf
>Of Yifan Lu Sent: Wednesday, October 24, 2012 9:11 AM To:
>[hidden email] Subject: Re: Deriving Formula from Ordinal
>Regression Results to Classify New Cases?
>
>Hi Vik,
>
>I just did some similar work recently. Basically once you have output
>from an Ordinal Regression, write down the formula in Y=
>a+b1X1+b2X2+...you should know a and bi from your output. Then
>use this formula in your excel sheet as a simulation model in excel,
>with X1, X2...as independent variables for clients to enter. Y is the
>predicted value.
>
>Hope this helps.
>
>Clare
>
>From: SPSSX(r) Discussion on behalf of Vik Rubenfeld Sent: Tue
>10/23/2012 8:30 PM To: [hidden email] Subject: Deriving
>Formula from Ordinal Regression Results to Classify New Cases?
>
>What is the correct method for deriving a formula from the results of
>an Ordinal Regression, that can be used to predict the value of the
>dependent variable for new cases?
>
>Thanks very much in advance to all for any info.
>
>Best,
>
>
>-Vik




--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

It is PLUM. Here is SPSS syntax of the kind I will be using:

DATASET ACTIVATE DataSet1.

PLUM CQIA9all BY CQIA5_1 CQIA5_2 CQIA5_3 CQIA6_1 CQIA6_2 CQIA6_3

  /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5) PCONVERGE(1.0E-6) SINGULAR(1.0E-8)

  /LINK=LOGIT

  /PRINT=FIT PARAMETER SUMMARY TPARALLEL

  /SAVE=PREDCAT.

On Oct 24, 2012, at 1:21 PM, David Marso wrote:

It would also be useful to know which SPSS procedure is to be used for the
analysis.
IIRC SPSS has NOMREG, PLUM , GENLIN and maybe others (hard to keep track of
all the players) which handle Nominal Response variables.   Do each of these
always result in the same results?  It would be interesting to know how to
ensure that the client is aware of the various assumptions and how to not
end up with GIGO by doing something unanticipated/off the reservation.  I
imagine things will really get dicey when you start trying to build Excel
spreadsheets which are also smart about categorical predictors and say
interactions...;-))
---

Maguin, Eugene wrote

My understanding is this: It's not the highest value per se. The computed

value is the log odds and you get one computed value for each level of the

DV excluding the reference level. Exponentiate those values to get the

odds. Then compute the probablility for each level. The formula is, I

think, (odds/(1+odds)). You will see one two results: 1) none of the

computed probabilities are greater than 0.5. Therefore the case goes in

the reference group. 2) One of the computed probabilities is greater than

0.5. Therefore the case goes in that group. Can two or more of the

computed probabilities be greater than 0.5?? I don't have enough

experience to say. There's others on the list that know a lot more about

this than I do. Perhaps they will comment.

Gene Maguin

-----Original Message-----

From: SPSSX(r) Discussion [mailto:

SPSSX-L@.UGA

] On Behalf Of Vik Rubenfeld

Sent: Wednesday, October 24, 2012 2:19 PM

To:

SPSSX-L@.UGA

Subject: Deriving Formula from Ordinal Regression Results to Classify New

Cases?

Hi Clare, Eugene,

Per Clare:

Y= a+b1X1+b2X2+..

Per Eugene:

The “y” that is computed is the log odds. I’d think you want to know

whether the probability of being in

the comparison group is greater than 0.5. If so there are a couple of

other

computational steps.

Would it be correct to compute Y, using the formula provided by Clare, for

each possible value of the DV, and then to select the value with the

highest Y as the predicted value for the DV?

Best,

-Vik

On Oct 24, 2012, at 7:03 AM, Maguin, Eugene wrote:

I may be misunderstanding some things but …

The “y” that is computed is the log odds. I’d think you want to know

whether the probability of being in the comparison group is greater

than 0.5. If so there are a couple of other computational steps.

Gene Maguin

From: SPSSX(r) Discussion [mailto:

SPSSX-L@.UGA

] On Behalf

Of Yifan Lu Sent: Wednesday, October 24, 2012 9:11 AM To:

SPSSX-L@.UGA

Subject: Re: Deriving Formula from Ordinal

Regression Results to Classify New Cases?

Hi Vik,

I just did some similar work recently. Basically once you have output

from an Ordinal Regression, write down the formula in Y=

a+b1X1+b2X2+...you should know a and bi from your output. Then

use this formula in your excel sheet as a simulation model in excel,

with X1, X2...as independent variables for clients to enter. Y is the

predicted value.

Hope this helps.

Clare

From: SPSSX(r) Discussion on behalf of Vik Rubenfeld Sent: Tue

10/23/2012 8:30 PM To:

SPSSX-L@.UGA

Subject: Deriving

Formula from Ordinal Regression Results to Classify New Cases?

What is the correct method for deriving a formula from the results of

an Ordinal Regression, that can be used to predict the value of the

dependent variable for new cases?

Thanks very much in advance to all for any info.

Best,

-Vik

--

View this message in context:

http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================

To manage your subscription to SPSSX-L, send a message to

LISTSERV@.UGA

(not to SPSSX-L), with no body text except the command. To leave the

list, send the command SIGNOFF SPSSX-L For a list of commands to manage

subscriptions, send the command INFO REFCARD

=====================

To manage your subscription to SPSSX-L, send a message to

LISTSERV@.UGA

(not to SPSSX-L), with no body text except the

command. To leave the list, send the command

SIGNOFF SPSSX-L

For a list of commands to manage subscriptions, send the command

INFO REFCARD

-----
Please reply to the list and not to my personal email.
Those desiring my consulting or training services please feel free to email me.
--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715852.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

I realized I could study this by examining the SPSS output.  SPSS has an option to produce the estimated probability for each possible value of the DV, for each case in the data file.  The DV has 5 possible values.

I ran the following syntax:

PLUM CQIA7 BY CQIA5_1 CQIA5_4 CQIA5_5 CQIA5_2 CQIA5_3 CQIA5_6 CQIA5_7
  /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5) PCONVERGE(1.0E-6) SINGULAR(1.0E-8)
  /LINK=LOGIT
  /PRINT=FIT PARAMETER SUMMARY TPARALLEL
  /SAVE=ESTPROB PREDCAT PCPROB ACPROB.

...and examined the estimated probabilities. It appears that the DV value with the highest probability becomes the predicted value for the DV. While I found cases in which no probability was greater than 0.5, I also found no cases where more than one value was greater than 0.5.  Interestingly, SPSS provides a probability for the reference group.

I will now use what I have learned from this thread to attempt to estimate probabilities within the same data file and compare them to SPSS-produced probabilities.

[Vik Rubenfeld]

I'm running a SPSS ordinal regression with just 2 predictor variables, in order to provide output for testing a suitable formula.  The syntax is:

PLUM CQIA7 BY CQIA5_3 CQIA5_4
  /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5) PCONVERGE(1.0E-6) SINGULAR(1.0E-8)
  /LINK=LOGIT
  /PRINT=FIT PARAMETER SUMMARY TPARALLEL
  /SAVE=ESTPROB PREDCAT PCPROB ACPROB.

Here is the output: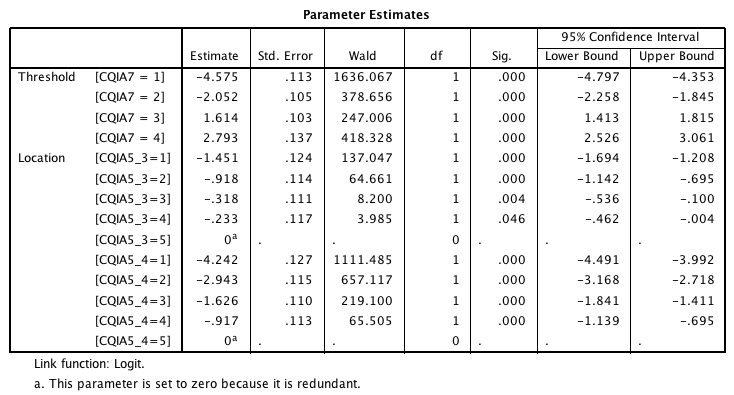



Here's what I've tried so far.

Let A = (observed value of predictor variable 1 *coefficient for observed value of predictor variable 1) + (observed value of predictor variable 2 * coefficient for observed value of predictor variable 2)

For each possible value of the DV:
--- Computed Value = A + threshold coefficient for that value of DV
--- Odds = exp(computed value)
--- Probability = odds/(1+odds)

So far my probabilities do not match the SPSS-computed probabilities.  

Where is my algorithm off the mark? Thanks very much in advance to all for any info!

Spreadsheet showing calculations as well as SPSS-computed probabilities for 10 cases:
Seeking_Formula_for_Predicting_Classification_via_Ordinal_Regression_Results.xlsx


==QUOTED FROM ADVICE KINDLY PROVIDED PREVIOUSLY IN THIS DISCUSSION==
Per Clare:

> Y= a+b1X1+b2X2+..

Per Eugene:

>The “y” that is computed is the log odds. I’d think you want to know
>whether the probability of being in the comparison group is greater than 0.5.
>If so there are a couple of other computational steps.

...

>My understanding is this: It's not the highest value per se. The
>computed value is the log odds and you get one computed value for
>each level of the DV excluding the reference level. Exponentiate
>those values to get the odds. Then compute the probablility for
>each level. The formula is, I think, (odds/(1+odds)). You will
>see one two results: 1) none of the computed probabilities are
>greater than 0.5. Therefore the case goes in the reference group.
>2) One of the computed probabilities is greater than 0.5.
>Therefore the case goes in that group. Can two or more of the
>computed probabilities be greater than 0.5?? I don't have enough
>experience to say. There's others on the list that know a lot
>more about this than I do. Perhaps they will comment.

[Fleming, Katie (DOT)]

Hello,

 

I am out of the office between October 29 through October 31. I will return messages on my return.

 

Thank you,

 

Katie

 

[Rich Ulrich]

From your output table, it is very apparent that PLUM is
doing something different from what you tried.  Notably,
the "probabilities" for PLUM do add up to 1.0 for each case.

I've never looked at the predictions from PLUM, but it
looks as if they might be similar to what I've seen for
discriminant function. 

Discriminant function is willing to list two "probabilities"
(or likelihoods?) for each case.  One is this ratio (hoping
I'm reconstructing it correctly from memory) -- For a
single function, it is based on the Mahalanobis distance
from each centroid.  It is the probability density for that
distance, divided by the maximum (value at the centroid). 
When a case is a multivariate outlier, this will be near 0
for every group.

The second one adjusts these previous numbers so that
they add up to 1.0.  That seems to be the sort of p's that
you listed, regardless of how some prior number was
achieved.

--
Rich Ulrich

> Date: Sun, 28 Oct 2012 15:54:35 -0700

> From: [hidden email]
> Subject: Re: Deriving Formula from Ordinal Regression Results to Classify New Cases?
> To: [hidden email]
>
> I'm running a SPSS ordinal regression with just 2 predictor variables, in
> order to provide output for testing a suitable formula. The syntax is:
>
> PLUM CQIA7 BY CQIA5_3 CQIA5_4
> /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5)
> PCONVERGE(1.0E-6) SINGULAR(1.0E-8)
> /LINK=LOGIT
> /PRINT=FIT PARAMETER SUMMARY TPARALLEL
> /SAVE=ESTPROB PREDCAT PCPROB ACPROB.
>
> Here is the output:
>
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5715904/Screen_shot_2012-10-28_at_2.52.43_PM.png>
>
> Here's what I've tried so far.
>
> Let A = (observed value of predictor variable 1 *coefficient for observed
> value of predictor variable 1) + (observed value of predictor variable 2 *
> coefficient for observed value of predictor variable 2)
>
> For each possible value of the DV:
> --- Computed Value = A + threshold coefficient for that value of DV
> --- Odds = exp(computed value)
> --- Probability = odds/(1+odds)
>
> So far my probabilities do not match the SPSS-computed probabilities.
>
> Where is my algorithm off the mark? Thanks very much in advance to all for
> any info!
>
> Spreadsheet showing calculations as well as SPSS-computed probabilities for
> 10 cases:
> Seeking_Formula_for_Predicting_Classification_via_Ordinal_Regression_Results.xlsx
> <http://spssx-discussion.1045642.n5.nabble.com/file/n5715904/Seeking_Formula_for_Predicting_Classification_via_Ordinal_Regression_Results.xlsx>
> ...

[Gonzales, Dana L]



I will be out of the office until Tuesday November 6th.

[David Marso]

"Let A = (observed value of predictor variable 1 *coefficient for observed value of predictor variable 1) + (observed value of predictor variable 2 * coefficient for observed value of predictor variable 2)"...

1. Try treating the predictors as dummy variables rather than as their numeric value!
2. To enhance the probability of acquiring assistance consider attaching a copy of the relevant data (the 3 variables only) and the predicted probabilities.  Also screen shots suck for anyone who might be willing to assist.

[Alex Reutter]

Vik,

A couple of quick notes:

1. Have a look at PLUM algorithms at: the http://pic.dhe.ibm.com/infocenter/spssstat/v21r0m0/topic/com.ibm.spss.statistics.help/alg_plum.htm.  That should help you write out the correct equations from the coefficients.

2. Are you really interested in writing out the equation yourself, or do you just want to score new records?  If the latter, then you probably want to build a model with GENLIN, output the model to a PMML file (http://pic.dhe.ibm.com/infocenter/spssstat/v21r0m0/topic/com.ibm.spss.statistics.help/syn_genlin_outfile.htm), and then use applymodel (http://pic.dhe.ibm.com/infocenter/spssstat/v21r0m0/topic/com.ibm.spss.statistics.help/syn_transformation_expressions_scoring_expressions.htm)

Alex

[Maguin, Eugene]

Vik,
Suppose you simplify your model to a dichotomous model that can run in the logistic regression proc. Can you reproduce the observed predicted crosstab? Actually, didn't you or somebody post a method for getting the predicted group membership using LR in the last few weeks?

Also, did/have you looked at the algorithms for Plum? There is a formula there for the predicted cell counts.


-----Original Message-----
From: SPSSX(r) Discussion [mailto:[hidden email]] On Behalf Of Vik Rubenfeld
Sent: Sunday, October 28, 2012 6:55 PM
To: [hidden email]
Subject: Re: Deriving Formula from Ordinal Regression Results to Classify New Cases?

I'm running a SPSS ordinal regression with just 2 predictor variables, in order to provide output for testing a suitable formula.  The syntax is:

PLUM CQIA7 BY CQIA5_3 CQIA5_4
  /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5)
PCONVERGE(1.0E-6) SINGULAR(1.0E-8)
  /LINK=LOGIT
  /PRINT=FIT PARAMETER SUMMARY TPARALLEL
  /SAVE=ESTPROB PREDCAT PCPROB ACPROB.

Here is the output:

<http://spssx-discussion.1045642.n5.nabble.com/file/n5715904/Screen_shot_2012-10-28_at_2.52.43_PM.png>

Here's what I've tried so far.

Let A = (observed value of predictor variable 1 *coefficient for observed value of predictor variable 1) + (observed value of predictor variable 2 * coefficient for observed value of predictor variable 2)

For each possible value of the DV:
--- Computed Value = A + threshold coefficient for that value of DV
--- Odds = exp(computed value)
--- Probability = odds/(1+odds)

So far my probabilities do not match the SPSS-computed probabilities.

Where is my algorithm off the mark? Thanks very much in advance to all for any info!

Spreadsheet showing calculations as well as SPSS-computed probabilities for
10 cases:
Seeking_Formula_for_Predicting_Classification_via_Ordinal_Regression_Results.xlsx
<http://spssx-discussion.1045642.n5.nabble.com/file/n5715904/Seeking_Formula_for_Predicting_Classification_via_Ordinal_Regression_Results.xlsx>


==QUOTED FROM ADVICE KINDLY PROVIDED PREVIOUSLY IN THIS DISCUSSION== Per Clare:

> Y= a+b1X1+b2X2+..

Per Eugene:

>The “y” that is computed is the log odds. I’d think you want to know
>whether the probability of being in the comparison group is greater
>than
0.5.
>If so there are a couple of other computational steps.

...

>My understanding is this: It's not the highest value per se. The
>computed value is the log odds and you get one computed value for each
>level of the DV excluding the reference level. Exponentiate those
>values to get the odds. Then compute the probablility for each level.
>The formula is, I think, (odds/(1+odds)). You will see one two results:
>1) none of the computed probabilities are greater than 0.5. Therefore
>the case goes in the reference group.
>2) One of the computed probabilities is greater than 0.5.
>Therefore the case goes in that group. Can two or more of the computed
>probabilities be greater than 0.5?? I don't have enough experience to
>say. There's others on the list that know a lot more about this than I
>do. Perhaps they will comment.

--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715904.html
Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to [hidden email] (not to SPSSX-L), with no body text except the command. To leave the list, send the command SIGNOFF SPSSX-L For a list of commands to manage subscriptions, send the command INFO REFCARD

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

Thanks to all who have pointed me in the direction of the SPSS algorithms used by PLUM.

As a market research specialist and a programmer, I don't easily read the formulas. I need to turn these formulas into an algorithm (e.g for each value of x, multiply a * b and divide by c, etc.) that I can then implement in Excel's Visual Basic programming language.

I would be delighted to hire someone for a few hours to walk me through this.  If anyone reading this would be available, please let me know. Alternatively, if anyone reading this knows of someone who might be available for this, please let me know. Thanks!

[Ryan]

Vik,

 

If you assume the proportional odds assumption and fit a cumulative logits model, then you can obtain the predicted probability for each category of the ordered response for each subject by employing a series of equations.

 

Let's assume you have four ordered categories, with the fourth category as the reference category, and you have three continuous predictors. The following series of equations will produce the predicted probability for each category for each subject:

 

eta1 = b0_1 + b1*x1 + b2*x2 + b3*x3

eta2 = b0_2 + b1*x1 + b2*x2 + b3*x3

eta3 = b0_3 + b1*x1 + b2*x2 + b3*x3

 

prob1 = 1 / [1 + exp(eta1)]

prob2 = 1 / [1 + exp(eta2)] - (1 / [1 + exp(eta1)])

prob3 = 1 / [1 + exp(eta3)] - (1 / [1 + exp(eta1)]) - (1 / [1 + exp(eta2)])

prob4 = 1 - (1 / [1 + exp(eta1)]) - (1 / [1 + exp(eta2)]) - (1 / [1 + exp(eta3)])

 

Admittedly, I have never used the PLUM procedure, but if you are fitting a cumulative logits model I would assume that plugging in the parameter estimates outputted from the procedure, along with values for the predictors for a given subject, into the linear predictors (eta1, eta2, eta3), and then transforming the linear predictors as demonstrated above should produce the probability for each category of the response for each subject.

 

The probabilities (prob1, prob2, prob3, prob4) should sum to 1.0 for each subject.

Ryan

On Mon, Oct 29, 2012 at 7:04 PM, Vik Rubenfeld <[hidden email]> wrote:

Thanks to all who have pointed me in the direction of the SPSS algorithms
used by PLUM.

As a market research specialist and a programmer, I don't easily read the
formulas. I need to turn these formulas into an algorithm (e.g for each
value of x, multiply a * b and divide by c, etc.) that I can then implement
in Excel's Visual Basic programming language.

I would be delighted to hire someone for a few hours to walk me through
this.  If anyone reading this would be available, please let me know.
Alternatively, if anyone reading this knows of someone who might be
available for this, please let me know. Thanks!



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715940.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Ryan]

Vik,

 

Scratch my last response. The equations were slightly off for a couple of reasons. I'm going to review the PLUM procedure and respond back with the solution when time permits. At first blush, it looks like the PLUM procedure estimates the probability of each category in ascending order. Shouldn't be difficult to figure out the equations--just need a little time, which happens to be a precious commodity these days.

 

More soon (unless somebody responds with the solution before I do)

 

Ryan

 

On Mon, Oct 29, 2012 at 9:16 PM, R B <[hidden email]> wrote:

Vik,

 

If you assume the proportional odds assumption and fit a cumulative logits model, then you can obtain the predicted probability for each category of the ordered response for each subject by employing a series of equations.

 

Let's assume you have four ordered categories, with the fourth category as the reference category, and you have three continuous predictors. The following series of equations will produce the predicted probability for each category for each subject:

 

eta1 = b0_1 + b1*x1 + b2*x2 + b3*x3

eta2 = b0_2 + b1*x1 + b2*x2 + b3*x3

eta3 = b0_3 + b1*x1 + b2*x2 + b3*x3

 

prob1 = 1 / [1 + exp(eta1)]

prob2 = 1 / [1 + exp(eta2)] - (1 / [1 + exp(eta1)])

prob3 = 1 / [1 + exp(eta3)] - (1 / [1 + exp(eta1)]) - (1 / [1 + exp(eta2)])

prob4 = 1 - (1 / [1 + exp(eta1)]) - (1 / [1 + exp(eta2)]) - (1 / [1 + exp(eta3)])

 

Admittedly, I have never used the PLUM procedure, but if you are fitting a cumulative logits model I would assume that plugging in the parameter estimates outputted from the procedure, along with values for the predictors for a given subject, into the linear predictors (eta1, eta2, eta3), and then transforming the linear predictors as demonstrated above should produce the probability for each category of the response for each subject.

 

The probabilities (prob1, prob2, prob3, prob4) should sum to 1.0 for each subject.

Ryan

On Mon, Oct 29, 2012 at 7:04 PM, Vik Rubenfeld <[hidden email]> wrote:

Thanks to all who have pointed me in the direction of the SPSS algorithms
used by PLUM.

As a market research specialist and a programmer, I don't easily read the
formulas. I need to turn these formulas into an algorithm (e.g for each
value of x, multiply a * b and divide by c, etc.) that I can then implement
in Excel's Visual Basic programming language.

I would be delighted to hire someone for a few hours to walk me through
this.  If anyone reading this would be available, please let me know.
Alternatively, if anyone reading this knows of someone who might be
available for this, please let me know. Thanks!



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715940.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

This is greatly appreciated!

[Ryan]

Vik,

 

Okay. I examined the PLUM procedure in the SPSS user guide....

 

Assuming the dependent variable consists of 4 ordered-categories (1, 2, 3, 4), here's how to calculate the cumulative probability of each category for each subject using the parameter estimates obtained from an ordinal regression model employed using the PLUM procedure:

 

eta1 = b0_1 - (b1*x1 + b2*x2 + b3*x3)

eta2 = b0_2 - (b1*x1 + b2*x2 + b3*x3)

eta3 = b0_3 - (b1*x1 + b2*x2 + b3*x3)

 

cum_prob_1 = 1 / [1 + exp(-eta1)]

cum_prob_1_2 = 1 / [1 + exp(-eta2)]

cum_prob_1_2_3 = 1 / [1 + exp(-eta3)]

cum_prob_1_2_3_4 = 1

 

Consequently, one can estimate category-specific probabilities for each subject as follows:

 

prob_1 = cum_prob_1

prob_2 = cum_prob_1_2 - cum_prob_1

prob_3 = cum_prob_1_3 - cum_prob_1_2

prob_4 = cum_prob_1_2_3_4 - cum_prob_1_2_3

 

The category with the highest probability (prob_1, prob_2, prob_3, or prob_4) should be the predicted category for that particular subject.

 

While I haven't tested any of the equations above, I'm fairly certain they are correct. Of course, you can and should test these equations by having the PLUM procedure output the probabilities for each subject, and then see if the equations above produce exactly the same estimates.

 

I bet they will. :-)

 

Oh!...one more point before I sign off from this thread...

 

Note that the estimated threshold parameters (b0_1, b0_2, b0_3) are permitted to vary across linear predictors (eta1, eta2, eta3), yet the estimated location parameters (b1, b2, b3) are not permitted to vary. This is at the heart the proportional odds assumption.

 

Best,

 

Ryan

On Mon, Oct 29, 2012 at 11:53 PM, Vik Rubenfeld <[hidden email]> wrote:

This is greatly appreciated!



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715943.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD

[Vik Rubenfeld]

Thank you very much! It is extremely kind of you and greatly appreciated. I will try this out and report back.

[Vik Rubenfeld]

In implementing:

    eta1 = b0_1 - (b1*x1 + b2*x2 + b3*x3)

...would I be correct in reading:

b0_1 = parameter estimate for threshold value = 1 (-4.575 in the example SPSS output below)
b1    = observed value in the input data for predictor variable 1 (e.g. a value 1-5 for a predictor variable  
           that can be a number 1 through 5)
x1    = parameter estimate for b1 (e.g., if b1 contains 3, -.318 in the example SPSS output below).

Also, if my reading is correct, what do I use as x1 if b1 contains the highest possible value, in which case there is no parameter estimate?

Thanks very much in advance for the info. I am looking forward to implementing the algorithm!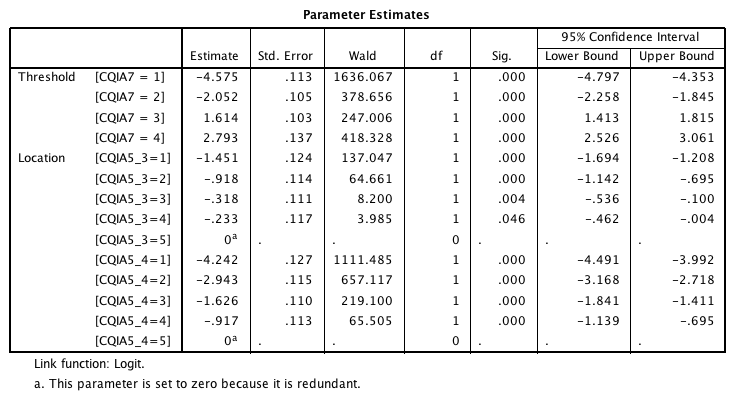

[Ryan]

Hi Vik,

 

The short answer is that you are misinterpreting the terms in the equations. I'll respond later today/tonight to help you achieve clarity.

 

Ryan

On Wed, Oct 31, 2012 at 1:29 AM, Vik Rubenfeld <[hidden email]> wrote:

In implementing:

    eta1 = b0_1 - (b1*x1 + b2*x2 + b3*x3)

...would I be correct in reading:

b0_1 = parameter estimate for threshold value = 1 (-4.575 in the example
SPSS output below)
b1    = observed value in the input data for predictor variable 1 (e.g. a
value 1-5 for a predictor variable
           that can be a number 1 through 5)
x1    = parameter estimate for b1 (e.g., if b1 contains 3, -.318 in the
example SPSS output below).

Also, if my reading is correct, what do I use as x1 if b1 contains the
highest possible value, in which case there is no parameter estimate?

Thanks very much in advance for the info. I am looking forward to
implementing the algorithm!

<http://spssx-discussion.1045642.n5.nabble.com/file/n5715962/Screen_shot_2012-10-28_at_2.52.43_PM.png>



--
View this message in context: http://spssx-discussion.1045642.n5.nabble.com/Deriving-Formula-from-Ordinal-Regression-Results-to-Classify-New-Cases-tp5715848p5715962.html

Sent from the SPSSX Discussion mailing list archive at Nabble.com.

=====================
To manage your subscription to SPSSX-L, send a message to
[hidden email] (not to SPSSX-L), with no body text except the
command. To leave the list, send the command
SIGNOFF SPSSX-L
For a list of commands to manage subscriptions, send the command
INFO REFCARD